题目内容
已知等腰三角形腰上的中线长为| 3 |
分析:根据题意画出图形,如图所示,设出等腰三角形的腰长为2a,根据D为AB中点,得到AD等于a,在三角形ADC中,利用余弦定理表示出cosA,解出a2,然后根据三角形的面积公式表示出三角形ADC的面积,并设面积为S,对表示出的面积两边求导数,令导函数等于0求出cosA的值,由cosA的值讨论导函数的正负,得到函数的单调区间,根据函数的增减性得到函数的最大值,且函数取得最大值时cosA的值,由cosA的值和A的范围,利用同角三角函数间的基本关系求出sinA的值,代入S中即可求出三角形ADC面积的最大值,又因为CD为三角形ABC的中线,所以由三角形ADC面积的最大值得到三角形ABC面积的最大值.
解答: 解:根据题意画出图形,如图所示:
解:根据题意画出图形,如图所示:
设AB=AC=2a,由D是AB的中点,得到AD=DB=a,
在△ADC中,根据余弦定理得:cosA=
=
,解得a2=
,
设△ADC的面积为S,
则S=
a•2a•sinA=a2sinA=
①,
.下研究求面积的最值
法一:求导得:S′=
=
,令S′=0,解得cosA=
,
当cosA<
时,S′>0,S单调递增;当cosA>
时,S′<0,S单调递减,
所以S在cosA=
处取极大值,且极大值为最大值,此时sinA=
,
所以S的最大值为
=1,
则△ABC的面积的最大值是2S=2.
法二:①式变形为5S-4ScosA=3sinA,可得5S=3sinA+4ScosA=
sin(A+θ),其中tanθ=
故有5S≤
,
解得S≤1,
则△ABC的面积的最大值是2S=2
故答案为:2.
 解:根据题意画出图形,如图所示:
解:根据题意画出图形,如图所示:设AB=AC=2a,由D是AB的中点,得到AD=DB=a,
在△ADC中,根据余弦定理得:cosA=
| a2+4a2-3 |
| 2×a×2a |
| 5a2-3 |
| 4a2 |
| 3 |
| 5-4cosA |
设△ADC的面积为S,
则S=
| 1 |
| 2 |
| 3sinA |
| 5-4cosA |
.下研究求面积的最值
法一:求导得:S′=
| 3cosA(5-4cosA)-12sin2A |
| (5-4cosA)2 |
| 15cosA-12 |
| (5-4cosA)2 |
| 4 |
| 5 |
当cosA<
| 4 |
| 5 |
| 4 |
| 5 |
所以S在cosA=
| 4 |
| 5 |
| 3 |
| 5 |
所以S的最大值为
3×
| ||
5-4×
|
则△ABC的面积的最大值是2S=2.
法二:①式变形为5S-4ScosA=3sinA,可得5S=3sinA+4ScosA=
| 9+16S2 |
| 4S |
| 3 |
故有5S≤
| 9+16S2 |
解得S≤1,
则△ABC的面积的最大值是2S=2
故答案为:2.
点评:此题考查学生灵活运用余弦定理及三角形的面积公式化简求值,会利用导数求闭区间上函数的最大值,掌握等腰三角形的性质,是一道中档题.

练习册系列答案
相关题目
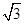 ,则该三角形的面积的最大值为( )
,则该三角形的面积的最大值为( ) C.
C. D.
D.
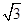 ,则该三角形的面积的最大值为 ▲ .
,则该三角形的面积的最大值为 ▲ .  ,则该三角形的面积的最大值是 .
,则该三角形的面积的最大值是 . ,则该三角形的面积的最大值是 .
,则该三角形的面积的最大值是 .