题目内容
已知函数f(x)=(x-2)2,f′(x)是函数f(x)的导函数,设由a1=3,an+1=an-
,
(1)求数列{an}的通项公式;
(2)令bn=nan,求数列{bn}的前n项和Sn.
| f(an) |
| f′(an) |
(1)求数列{an}的通项公式;
(2)令bn=nan,求数列{bn}的前n项和Sn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(I)f′(x)=2(x-2),由an+1=an-
,可得an+1=an-
,变形an+1-2=
(an-2),利用等比数列的通项公式即可得出.
(Ⅱ)由题意bn=nan=
+2n,再利用“错位相减法”、等比数列的前n项和公式即可得出.
| f(an) |
| f′(an) |
| (an-2)2 |
| 2(an-2) |
| 1 |
| 2 |
(Ⅱ)由题意bn=nan=
| n |
| 2n-1 |
解答:
解:(I)f′(x)=2(x-2),由an+1=an-
,
可得an+1=an-
,化为an+1=
an+1,变形an+1-2=
(an-2),
∴{an-2}是以a1-2=1为首项,公比为
的等比数列,
∴an-2=(a1-2)•(
)n-1,
∴an=2+(
)n-1.
(Ⅱ)由题意bn=nan=
+2n,
设数列{
}的前n项和为Tn,
则Tn=1+
+
+…+
,
Tn=
+
+
+…
+
,
Tn=1+
+
+…+
-
=
-
=2-
,
即Tn=4-
,
∴Sn=Tn+n2+n=4-
+n2+n.
| f(an) |
| f′(an) |
可得an+1=an-
| (an-2)2 |
| 2(an-2) |
| 1 |
| 2 |
| 1 |
| 2 |
∴{an-2}是以a1-2=1为首项,公比为
| 1 |
| 2 |
∴an-2=(a1-2)•(
| 1 |
| 2 |
∴an=2+(
| 1 |
| 2 |
(Ⅱ)由题意bn=nan=
| n |
| 2n-1 |
设数列{
| n |
| 2n-1 |
则Tn=1+
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n-1 |
| 2n-1 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| n |
| 2n |
1-
| ||
1-
|
| n |
| 2n |
| 2+n |
| 2n |
即Tn=4-
| 2+n |
| 2n-1 |
∴Sn=Tn+n2+n=4-
| n+2 |
| 2n-1 |
点评:本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=x3-2x,若f(a)+f(b)=0,则a+b的值为( )
| A、1 | B、0 | C、-1 | D、不能确定 |
若焦点在y轴上的双曲线的渐近线方程是y=±2x,则该双曲线的离心率是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设函数f(x)是定义在R上的奇函数,且满足f(3+x)=f(3-x),当x∈(0,3)时,f(x)=2x,则f(-5)=( )
| A、2 | ||
B、-
| ||
| C、-2 | ||
D、
|
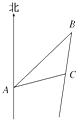 某海域内一观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东50°且与A相距80海里的位置B,经过1小时又测得该船已行驶到点A北偏东50°+θ其中sin θ=
某海域内一观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东50°且与A相距80海里的位置B,经过1小时又测得该船已行驶到点A北偏东50°+θ其中sin θ=