题目内容
双曲线 ,点M在双曲线上,△F1MF2的面积为
,点M在双曲线上,△F1MF2的面积为 ,
,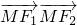 等于
等于
- A.2
- B.-2
- C.

- D.-

A
分析:由△F1MF2的面积s= =
= 可求h即点M的综坐标,代入可求M的 横坐标,最后利用向量的数量积的坐标表示即可求解
可求h即点M的综坐标,代入可求M的 横坐标,最后利用向量的数量积的坐标表示即可求解
解答:设M(x,y),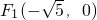 ,F2(
,F2( )
)
∴
∵△F1MF2的面积s= =
=
∴ ,则|yM|=
,则|yM|= ,代入到双曲线方程中可得
,代入到双曲线方程中可得
∵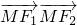 =
= •(
•( ,-y)=x2+y2-5=2
,-y)=x2+y2-5=2
故选A
点评:本题主要考查了双曲线的性质的简单应用,向量的数量积的 坐标表示的应用
分析:由△F1MF2的面积s=
 =
= 可求h即点M的综坐标,代入可求M的 横坐标,最后利用向量的数量积的坐标表示即可求解
可求h即点M的综坐标,代入可求M的 横坐标,最后利用向量的数量积的坐标表示即可求解解答:设M(x,y),
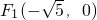 ,F2(
,F2( )
)∴

∵△F1MF2的面积s=
 =
=
∴
 ,则|yM|=
,则|yM|= ,代入到双曲线方程中可得
,代入到双曲线方程中可得
∵
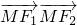 =
= •(
•( ,-y)=x2+y2-5=2
,-y)=x2+y2-5=2故选A
点评:本题主要考查了双曲线的性质的简单应用,向量的数量积的 坐标表示的应用

练习册系列答案
相关题目
 ,点M在双曲线上,△F1MF2的面积为
,点M在双曲线上,△F1MF2的面积为 ,
, 等于()
等于() ,点M在双曲线上,△F1MF2的面积为
,点M在双曲线上,△F1MF2的面积为 ,
,