题目内容
已知椭圆:()过点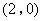 ,且椭圆的离心率为.
,且椭圆的离心率为.
(Ⅰ)求椭圆的方程;
(Ⅱ)若动点在直线上,过作直线交椭圆于两点,且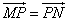 ,再过作直线.证明:直线恒过定点,并求出该定点的坐标.
,再过作直线.证明:直线恒过定点,并求出该定点的坐标.
解:(Ⅰ)因为点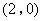 在椭圆
在椭圆 上,所以
上,所以 , 所以
, 所以 ,
,
因为椭圆 的离心率为
的离心率为 , 所以
, 所以 ,即
,即 ,
,
解得 ,
,
所以椭圆 的方程为
的方程为 .
.
(Ⅱ)设 ,
, ,
,
①当直线 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为 ,
, ,
, ,
,
由 得
得 ,
,
所以 ,
,
因为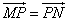 ,即
,即 为
为 中点,所以
中点,所以 ,即
,即 .
.
所以 ,
,
因为直线 , 所以
, 所以 ,所以直线
,所以直线 的方程为
的方程为 ,
,
即 ,显然直线
,显然直线 恒过定点
恒过定点 .
.
②当直线 的斜率不存在时,直线
的斜率不存在时,直线 的方程为
的方程为 ,
,
此时直线 为
为 轴,也过点
轴,也过点 .
.
综上所述直线 恒过定点
恒过定点 .
.

练习册系列答案
相关题目
用 到
到 这
这 个数字,可以组成没有重复数字的三位偶数的个数为( )
个数字,可以组成没有重复数字的三位偶数的个数为( )
| A. | B. | C. | D. |
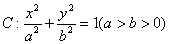 的左、右焦点,
的左、右焦点,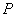 为椭圆
为椭圆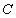 上任意一点,且
上任意一点,且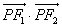 的最小值为
的最小值为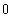 ,则椭圆的离心率为
,则椭圆的离心率为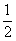 (B)
(B)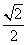 (C)
(C)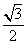 (D)
(D)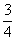
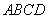 中有一个不规则的图形
中有一个不规则的图形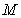 ,用随机模拟方法来估计不规则图形的面积.若在正方形
,用随机模拟方法来估计不规则图形的面积.若在正方形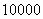 个点,落在不规则图形
个点,落在不规则图形



 与
与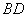 所成的角的度数为 ,当三棱锥的体积取得最大值时, 四棱锥
所成的角的度数为 ,当三棱锥的体积取得最大值时, 四棱锥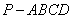 的高
的高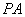 的长为 .
的长为 .
 与x轴切于A点,与y轴切于B点,设劣弧
与x轴切于A点,与y轴切于B点,设劣弧 的中点为M,则过点M的圆C的切线方程是( )
的中点为M,则过点M的圆C的切线方程是( ) (B)
(B) (C)
(C) (D)
(D)
 的值为
的值为  B.
B. C.
C. D.
D.