题目内容
在某种产品表面进行腐蚀性试验,得到腐蚀深度y与腐蚀时间t之间对应的一组数据：时间t(s) | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 90 | 120 |
深度y(μm) | 6 | 10 | 10 | 13 | 16 | 17 | 19 | 23 | 25 | 29 | 46 |
(1)画出散点图.
(2)求腐蚀深度y对腐蚀时间t的回归直线方程.
(3)试预测腐蚀时间为100 s时,腐蚀深度是多少.
分析：本题考查线性回归直线方程的求法及意义.
先画出其散点图,看其是否呈直线形,再依系数a、b的计算公式,算出a、b的值,写出回归直线方程.由时间的t值求出
值.
解：(1)散点图为
(2)经计算可得
故所求的线性回归方程为
=0.304x+5.36.
(3)根据上面所求得的回归直线方程,当腐蚀时间为100 s时, 
=0.304×100+5.36=35.76(μm),即腐蚀深度大约是35.76 μm.
点评：(1)对一组数据进行线性回归分析时,应先画出其散点图,看其是否呈直线形,如果呈直线形,再依系数a、b的计算公式,算出a、b的值,写出回归直线方程.
(2)由回归直线方程对两个变量间的线性相关关系进行研究,实际上是将非确定性的相关关系问题转化成确定性的函数关系问题进行研究.
阅读快车系列答案| 时间x（秒） | 5 | 10 | 15 | 20 | 30 | 40 |
| 深度（微米） | 6 | 10 | 10 | 13 | 16 | 17 |
（Ⅰ）求选取的2组数据恰好不相邻的概率；
（Ⅱ）若选取的是第2组和第5组数据，根据其它4组数据，求得y关于x的线性回归方程
| ? |
| y |
| 4 |
| 13 |
| 139 |
| 26 |
（本小题满分12分）
在某种产品表面进行腐蚀性检验，得到腐蚀深度
与腐蚀时间
之间对应的一组数据：
| 时间 | 5 | 10 | 15 | 20 | 30 | 40 |
| 深度 | 6 | 10 | 10 | 13 | 16 | 17 |
现确定的研究方案是：先从这6组数据中选取2组，用剩下的4组数据求线性回归方程，再对被选取的2组数据进行检验．
（Ⅰ）求选取的2组数据恰好不相邻的概率；
（Ⅱ）若选取的是第2组和第5组数据，根据其它4组数据，求得关于的线性回归方程
，规定由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2微米，则认为得到的线性回归方程是可靠的，判断该线性回归方程是否可靠．
（本小题满分12分）
在某种产品表面进行腐蚀性检验，得到腐蚀深度
与腐蚀时间
之间对应的一组数据：
| 时间 | 5 | 10 | 15 | 20 | 30 | 40 |
| 深度 | 6 | 10 | 10 | 13 | 16 | 17 |
现确定的研究方案是：先从这6组数据中选取2组，用剩下的4组数据求线性回归方程，再对被选取的2组数据进行检验．
（Ⅰ）求选取的2组数据恰好不相邻的概率；
（Ⅱ）若选取的是第2组和第5组数据，根据其它4组数据，求得关于的线性回归方程
，规定由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2微米，则认为得到的线性回归方程是可靠的，判断该线性回归方程是否可靠．
| 时间x（秒） | 5 | 10 | 15 | 20 | 30 | 40 |
| 深度（微米） | 6 | 10 | 10 | 13 | 16 | 17 |
（Ⅰ）求选取的2组数据恰好不相邻的概率；
（Ⅱ）若选取的是第2组和第5组数据，根据其它4组数据，求得y关于x的线性回归方程
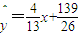，规定由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2微米，则认为得到的线性回归方程是可靠的，判断该线性回归方程是否可靠．