Question

在某种产品表面进行腐蚀性检验，得到腐蚀深度x与腐蚀时间x之间对应的一组数据：

时间x（秒）	5	10	15	20	30	40
深度（微米）	6	10	10	13	16	17

现确定的研究方案是：先从这6组数据中选取2组，用剩下的4组数据求线性回归方程，再对被选取的2组数据进行检验．
（Ⅰ）求选取的2组数据恰好不相邻的概率；
（Ⅱ）若选取的是第2组和第5组数据，根据其它4组数据，求得y关于x的线性回归方程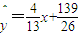，规定由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2微米，则认为得到的线性回归方程是可靠的，判断该线性回归方程是否可靠．

Answer 1

【答案】分析：（Ⅰ）设6组数据的编号分别为1，2，3，4，5，6，从6组数据中选取2组数据共有15种情况，满足条件的事件是抽到不相邻的两组数据，列举出共有10种结果，得到概率．
（II）代入所给的x的值，预报出对应的y的值，把求得的y的值和所给的准确数值进行比较．得到差的绝对值小于2，得到结论．
解答：解：（Ⅰ）设6组数据的编号分别为1，2，3，4，5，6．设抽到不相邻的两组数据为事件A，
从6组数据中选取2组数据共有15种情况：（1，2）（1，3）（1，4）（1，5）（1，6）
（2，3）（2，4）（2，5）（2，6）（3，4）（3，5）（3，6）（4，5）（4，6）（5，6），
其中事件A包含的基本事件有10种．        …（3分）
所以．
所以选取的2组数据恰好不相邻的概率是． …（6分）
（Ⅱ） 当x=10时，；…（9分）
当x=30时，；
∴该研究所得到的回归方程是可靠的．            …（12分）
点评：本题考查线性回归方程的应用，在解题过程中注意对于预报值的估计，本题是一个基础题，若出现一定是一个得分题目．