题目内容
【题目】为了解学生自主学习期间完成数学套卷的情况，一名教师对某班级的所有学生进行了调查，调查结果如下表.
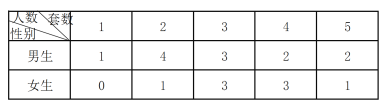
（1）从这班学生中任选一名男生，一名女生，求这两名学生完成套卷数之和为4的概率？
（2）若从完成套卷数不少于4套的学生中任选4人，设选到的男学生人数为
，求随机变量的分布列和数学期望；
（3）试判断男学生完成套卷数的方差
与女学生完成套卷数的方差
的大小（只需写出结论）.
【答案】（1）
（2）详见解析（3）
【解析】
(1)根据组合的方法求解所有可能的情况与满足条件的情况数再计算概率即可.
(2)
的取值为0,1,2,3,4.再根据超几何分布的方法求分布列与数学期望即可.
(3)直接根据数据观察稳定性判断
与
的大小即可.
解：（1）设事件
：从这个班级的学生中随机选取一名男生,一名女生,这两名学生完成套卷数之和为4,
由题意可知,
.
（2）完成套卷数不少于4本的学生共8人,其中男学生人数为4人,故的取值为0,1,2,3,4.
由题意可得
；
；
；
；
.
所以随机变量的分布列为
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
随机变量的均值
.
(3).
练习册系列答案
黄冈冠军课课练系列答案
相关题目
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计，绘制了频率分布直方图（如图所示）.规定80分及以上者晋级成功，否则晋级失败（满分100分）.
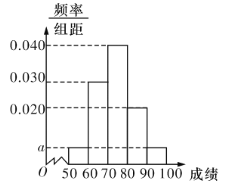
（1）求图中
的值；
（2）根据已知条件完成下面
列联表，并判断能否有
的把握认为“晋级成功”与性别有关？
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
（参考公式：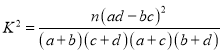
，其中
）
| 0.40 | 0.025 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
（3）将频率视为概率，从本次考试80分以上的所有人员中，按分层抽样的方式抽取5个人的样本；现从5人样本中随机选取2人，求选取的2人恰好都来自区间
的概率.
