题目内容
【题目】已知椭圆C中心在原点，离心率 
，其右焦点是圆E：（x﹣1）2+y2=1的圆心． 
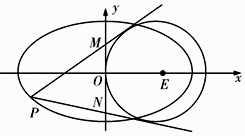
（1）求椭圆C的标准方程；
（2）如图，过椭圆C上且位于y轴左侧的一点P作圆E的两条切线，分别交y轴于点M、N．试推断是否存在点P，使 
？若存在，求出点P的坐标；若不存在，请说明理由．
【答案】
（1）解：设椭圆方程 
=1（a＞b＞0），半焦距为c，
因为椭圆的右焦点是圆E的圆心，则c=1，
因为椭圆的离心率为 
，则 
，即a= 
，
从而b2=a2﹣c2=1，
故椭圆C的方程为 
（2）解：设点P（x0，y0）（x0＜0），M（0，m），N（0，n），
则直线PM的方程为y= 
，即（y0﹣m）x﹣x0y+mx0=0，
因为圆心E（1，0）到直线PM的距离为1，
即 
=1，
即（y0﹣m）2+ 
=（y0﹣m）2+2x0m（y0﹣m）+ 
，即（x0﹣2）m2+2y0m﹣x0=0，
同理（x0﹣2）n2+2y0n﹣x0=0．
由此可知，m，n为方程（x0﹣2）x2+2y0x﹣x0=0的两个实根，
所以m+n=﹣ 
，mn=﹣ 
，
|MN|=|m﹣n|= 
= 
= 
．
因为点P（x0，y0）在椭圆C上，则 
，即 
，
则|MN|= 
= 
= 
，
令 = 
，
则（x0﹣2）2=9，
因为x0＜0，则x0=﹣1， 
=1﹣ 
= 
，即 
，
故存在点P（﹣1， 
）满足题设条件
【解析】（1）由已知条件分别求出a，c的值，而b2=a2﹣c2 ， 代入求出椭圆的方程．（2）假设存在点P满足题意，设点P（x0 ， y0）（x0＜0），M（0，m），N（0，n），利用条件求出直线PM方程，根据圆心E（1，0）到直线．的距离为1，求出m与点P坐标之间的关系，同理求出n与点P坐标之间的关系，利用韦达定理求出m+n，mn的表达式，算出|MN|，求出P点坐标．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
．
