题目内容
已知椭圆方程为
思路分析:本题为求点的轨迹方程问题,求点的轨迹方程问题用一般方法可以求解,直接寻找点的横、纵坐标间的关系较麻烦,利用参数方程,寻求横、纵坐标间的间接关系,然后消去参数的方法则相对较简单,即消参法求轨迹方程,是求轨迹的一种常用方法.
解:设椭圆的参数方程为![]() (θ为参数,且0≤θ<2π).则P点坐标为(acosθ,bsinθ),由题意知cosθ≠1,sinθ≠0.
(θ为参数,且0≤θ<2π).则P点坐标为(acosθ,bsinθ),由题意知cosθ≠1,sinθ≠0.
∵![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,![]() =
=![]() .
.
∴A1Q的方程为y=![]() (x+a),①
(x+a),①
A2Q的方程为y=![]() (x-a).②
(x-a).②
①×②,得y2=![]() ·(x2-a2)=
·(x2-a2)=![]() (x2-a2).
(x2-a2).
化简整理,得 1(λ≠0),即为所求的轨迹方程.
1(λ≠0),即为所求的轨迹方程.

练习册系列答案
相关题目
 +
+ =1(a>b>0),O为原点,F为右焦点,点M是椭圆右准线l上(除去与x轴的交点)的动点,过F作OM的垂线与以OM为直径的圆交于点N,则线段ON的长为
=1(a>b>0),O为原点,F为右焦点,点M是椭圆右准线l上(除去与x轴的交点)的动点,过F作OM的垂线与以OM为直径的圆交于点N,则线段ON的长为 +
+ =1,则其离心率为 .
=1,则其离心率为 .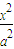 +
+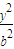 =1(a>b>0),O为原点,F为右焦点,点M是椭圆右准线l上(除去与x轴的交点)的动点,过F作OM的垂线与以OM为直径的圆交于点N,则线段ON的长为( )
=1(a>b>0),O为原点,F为右焦点,点M是椭圆右准线l上(除去与x轴的交点)的动点,过F作OM的垂线与以OM为直径的圆交于点N,则线段ON的长为( ) +
+ =1(a>b>0),O为原点,F为右焦点,点M是椭圆右准线l上(除去与x轴的交点)的动点,过F作OM的垂线与以OM为直径的圆交于点N,则线段ON的长为( )
=1(a>b>0),O为原点,F为右焦点,点M是椭圆右准线l上(除去与x轴的交点)的动点,过F作OM的垂线与以OM为直径的圆交于点N,则线段ON的长为( )