题目内容
已知函数 ,其中
,其中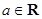 .
.
(1)当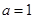 时,求曲线
时,求曲线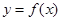 在原点处的切线方程;
在原点处的切线方程;
(2)求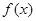 的单调区间.
的单调区间.
 ,其中
,其中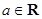 .
.(1)当
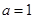 时,求曲线
时,求曲线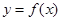 在原点处的切线方程;
在原点处的切线方程;(2)求
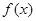 的单调区间.
的单调区间.(1)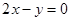
(2)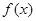 的单调增区间是
的单调增区间是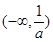 ,
,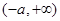 ;单调减区间是
;单调减区间是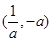
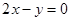
(2)
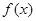 的单调增区间是
的单调增区间是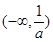 ,
,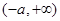 ;单调减区间是
;单调减区间是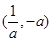
本试题主要是考查导数在研究函数中的 运用求解函数的单调性和函数的切线方程的 综合运用。
(1)先求解函数在该点的导数值,然后得到斜率和点的坐标,进而利用点斜式得到直线的方程。
(2)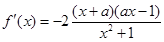
对于参数a分为大于零,小于零,等于零三种情况分析讨论单调性得到结论。
解:(1)当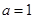 时,
时,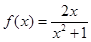 ,
,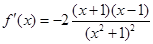 . ……………2分
. ……………2分
由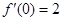 , 得曲线
, 得曲线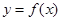 在原点处的切线方程是
在原点处的切线方程是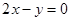 .………4分
.………4分
(2)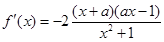 .……………5分
.……………5分
① 当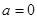 时,
时,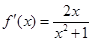 .
.
所以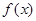 在
在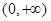 单调递增,在
单调递增,在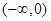 单调递减. ……7分
单调递减. ……7分
当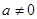 ,
,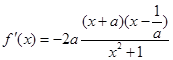 .
.
② 当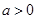 时,令
时,令 ,得
,得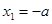 ,
,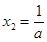 ,
,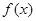 与
与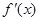 的情况如下:
的情况如下:
故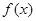 的单调减区间是
的单调减区间是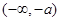 ,
,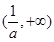 ;单调增区间是
;单调增区间是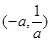 .…10分
.…10分
③ 当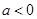 时,
时,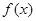 与
与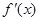 的情况如下:
的情况如下:
所以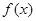 的单调增区间是
的单调增区间是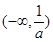 ,
,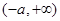 ;单调减区间是
;单调减区间是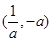 ………12分
………12分
(1)先求解函数在该点的导数值,然后得到斜率和点的坐标,进而利用点斜式得到直线的方程。
(2)
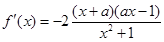
对于参数a分为大于零,小于零,等于零三种情况分析讨论单调性得到结论。
解:(1)当
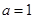 时,
时,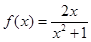 ,
,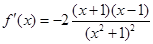 . ……………2分
. ……………2分由
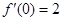 , 得曲线
, 得曲线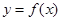 在原点处的切线方程是
在原点处的切线方程是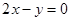 .………4分
.………4分 (2)
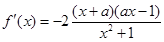 .……………5分
.……………5分① 当
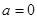 时,
时,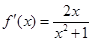 .
.所以
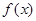 在
在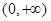 单调递增,在
单调递增,在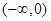 单调递减. ……7分
单调递减. ……7分当
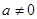 ,
,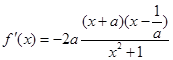 .
.② 当
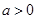 时,令
时,令 ,得
,得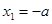 ,
,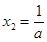 ,
,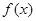 与
与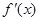 的情况如下:
的情况如下: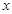 | 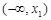 | 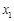 |  | 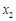 | 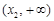 |
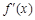 |  |  | 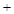 |  |  |
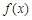 | ↘ | 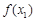 | ↗ | 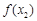 | ↘ |
故
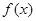 的单调减区间是
的单调减区间是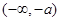 ,
,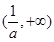 ;单调增区间是
;单调增区间是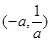 .…10分
.…10分③ 当
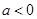 时,
时,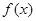 与
与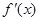 的情况如下:
的情况如下: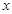 | 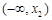 | 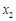 | 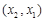 | 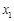 | 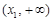 |
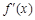 | 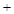 |  |  |  | 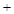 |
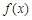 | ↗ | 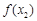 | ↘ | 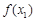 | ↗ |
所以
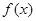 的单调增区间是
的单调增区间是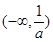 ,
,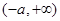 ;单调减区间是
;单调减区间是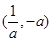 ………12分
………12分 
练习册系列答案
相关题目

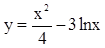 的一条切线的斜率为
的一条切线的斜率为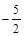 ,则切点的坐标为 ;
,则切点的坐标为 ;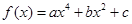 满足
满足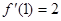 ,则
,则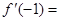 ( )
( )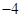
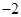
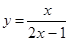 在点
在点 处的切线为l,则l上的点到
处的切线为l,则l上的点到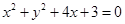 上的
上的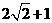

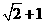
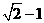
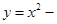 lnx上任意一点,则点P到直线y=x+3的最小距离为( )
lnx上任意一点,则点P到直线y=x+3的最小距离为( ) 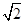
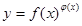 的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得 ,两边对
,两边对 求导数,得
求导数,得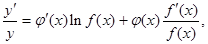 于是
于是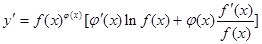 ,运用此方法可以求得函数
,运用此方法可以求得函数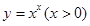 在(1,1)处的切线方程是 _________
在(1,1)处的切线方程是 _________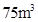 ,墙高为
,墙高为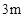 的长方体形的简易仓库. 已知仓库屋顶每平方米的造价为500元,墙壁每平方米的造价为400元,地面造价忽略不计. 问怎样设计仓库地面的长与宽,能使总造价最低?最低造价是多少?
的长方体形的简易仓库. 已知仓库屋顶每平方米的造价为500元,墙壁每平方米的造价为400元,地面造价忽略不计. 问怎样设计仓库地面的长与宽,能使总造价最低?最低造价是多少?
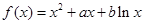 (
(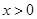 ,实数
,实数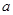 ,
,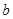 为常数).
为常数).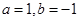 ,求
,求 在
在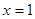 处的切线方程;
处的切线方程;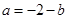 ,讨论函数
,讨论函数