题目内容
如图,有一块等腰直角三角形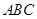 的空地,要在这块空地上开辟一个内接矩形
的空地,要在这块空地上开辟一个内接矩形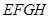 的绿地,已知
的绿地,已知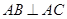 ,
,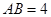 ,绿地面积最大值为( )
,绿地面积最大值为( )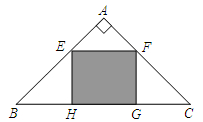
A.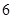 | B.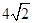 | C. | D.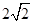 |
C
解析试题分析:设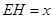 ,
,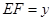 ,由条件可知
,由条件可知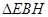 和
和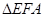 为等直角三角形,所以
为等直角三角形,所以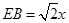 ,
,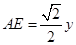 .
.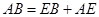 =
=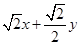 ≥
≥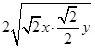 =
=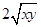 ,即
,即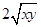 ≤4,所以
≤4,所以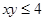 ,所以绿地面积最大值为4,故选C.
,所以绿地面积最大值为4,故选C.
考点:基本不等式在实际中的应用.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
对任意正数x,y不等式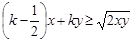 恒成立,则实数
恒成立,则实数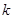 的最小值是 ( )
的最小值是 ( )
| A.1 | B.2 | C.3 | D.4 |
下列结论正确的是 ( )
A.当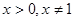 时, 时,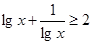 |
B.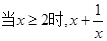 的最小值为 的最小值为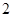 |
C.当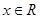 时, 时,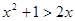 |
D.当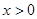 时, 时,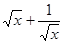 的最小值为 的最小值为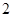 |
若实数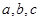 满足
满足 ,则
,则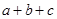 的最大值为( )
的最大值为( )
| A.9 | B. | C.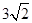 | D.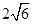 |
已知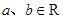 ,且
,且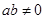 ,则下列结论恒成立的是 ( ).
,则下列结论恒成立的是 ( ).
A.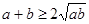 | B.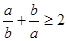 | C.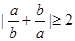 | D.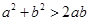 |
设椭圆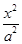 +
+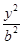 =1和x轴正半轴交点为A,和y轴正半轴的交点为B,P为第一象限内椭圆上的点,那么四边形OAPB面积最大值为 ( )
=1和x轴正半轴交点为A,和y轴正半轴的交点为B,P为第一象限内椭圆上的点,那么四边形OAPB面积最大值为 ( )
A. ab ab | B.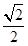 ab ab | C.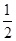 ab ab | D.2ab |
已知 ,则
,则 的最小值是( )
的最小值是( )
| A.4 |
| B.3 |
| C.2 |
| D.1 |
“x>0”是“x+ ≥2”的( )
≥2”的( )
| A.充分但不必要条件 |
| B.必要但不充分条件 |
| C.充分且必要条件 |
| D.既不充分也不必要条件 |
不等式x2+2x<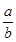 +
+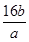 对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )
对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )
| A.(-2,0) | B.(-∞,-2)∪(0,+∞) |
| C.(-4,2) | D.(-∞,-4)∪(2,+∞) |