题目内容
直线l1:7x-y+4=0到l2:x+y-2=0的角平分线方程是
- A.6x+2y-3=0或x-3y+7=0
- B.6x+2y+3=0
- C.x+3y+7=0
- D.6x+2y-3=0
D
分析:先求出两直线的交点坐标,设直线l1:7x-y+4=0到l2:x+y-2=0的角平分线的斜率等于k,则有 =
=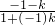 ,解得 k=-3,或 k=
,解得 k=-3,或 k= .再由直线l1到角平分线的夹角应是锐角可得
.再由直线l1到角平分线的夹角应是锐角可得  ,从而进一步确定k的值,由点斜式求得角平分线方程.
,从而进一步确定k的值,由点斜式求得角平分线方程.
解答:由 解得
解得  ,故两直线的交点为(
,故两直线的交点为( ).
).
设直线l1:7x-y+4=0到l2:x+y-2=0的角平分线的斜率等于k,则直线l1到角平分线的夹角等于角平分线到直线l2的夹角.
∴ =
=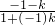 ,解得 k=-3,或 k=
,解得 k=-3,或 k= .
.
再由直线l1到角平分线的夹角应是锐角可得 ,∴k=-3.
,∴k=-3.
由点斜式求得角平分线方程是 y- =-3(x+
=-3(x+ ),即 6x+2y-3=0,
),即 6x+2y-3=0,
故选D.
点评:本题主要考查一条直线到另一条直线的夹角公式的应用,用点斜式求直线方程,注意直线l1到角平分线的夹角应是锐角,它的正切值 ,这是解题的易错点,容易错选A,属于中档题.
,这是解题的易错点,容易错选A,属于中档题.
分析:先求出两直线的交点坐标,设直线l1:7x-y+4=0到l2:x+y-2=0的角平分线的斜率等于k,则有
 =
=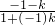 ,解得 k=-3,或 k=
,解得 k=-3,或 k= .再由直线l1到角平分线的夹角应是锐角可得
.再由直线l1到角平分线的夹角应是锐角可得  ,从而进一步确定k的值,由点斜式求得角平分线方程.
,从而进一步确定k的值,由点斜式求得角平分线方程.解答:由
 解得
解得  ,故两直线的交点为(
,故两直线的交点为( ).
).设直线l1:7x-y+4=0到l2:x+y-2=0的角平分线的斜率等于k,则直线l1到角平分线的夹角等于角平分线到直线l2的夹角.
∴
 =
=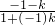 ,解得 k=-3,或 k=
,解得 k=-3,或 k= .
.再由直线l1到角平分线的夹角应是锐角可得
 ,∴k=-3.
,∴k=-3.由点斜式求得角平分线方程是 y-
 =-3(x+
=-3(x+ ),即 6x+2y-3=0,
),即 6x+2y-3=0,故选D.
点评:本题主要考查一条直线到另一条直线的夹角公式的应用,用点斜式求直线方程,注意直线l1到角平分线的夹角应是锐角,它的正切值
 ,这是解题的易错点,容易错选A,属于中档题.
,这是解题的易错点,容易错选A,属于中档题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目