题目内容
设
,
是夹角为60°的单位向量,若
是单位向量,则(
-
)•(
+
)的取值范围( )
| a |
| b |
| c |
| a |
| c |
| b |
| c |
分析:通过建立直角坐标系写出向量的坐标,进而转化为求三角函数的取值范围即可.
解答:解:建立如图所示的坐标系,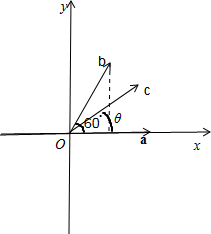
则
=(1,0),
=(
,
),
设向量
与x轴的夹角为θ,则
=(cosθ,sinθ).θ∈[0,2π).
则
-
=(1-cosθ,-sinθ),
+
=(
+cosθ,
+sinθ).
∴(
-
)•(
+
)=(1-cosθ)(
+cosθ)+(
+sinθ)(-sinθ)
=-
+
cosθ-
sinθ
=sin(
-θ)-
∵-1≤sin(
-θ)≤1,∴-
≤sin(
-θ)≤
.
∴(
-
)•(
+
)的取值范围是[-
,
].
故选C.

则
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
设向量
| c |
| c |
则
| a |
| c |
| b |
| c |
| 1 |
| 2 |
| ||
| 2 |
∴(
| a |
| c |
| b |
| c |
| 1 |
| 2 |
| ||
| 2 |
=-
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=sin(
| π |
| 6 |
| 1 |
| 2 |
∵-1≤sin(
| π |
| 6 |
| 3 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
∴(
| a |
| c |
| b |
| c |
| 3 |
| 2 |
| 1 |
| 2 |
故选C.
点评:熟练掌握向量的坐标运算、数量积和三角函数的取值范围是解题的关键.

练习册系列答案
相关题目