题目内容
【题目】已知函数![]() 的最大值为
的最大值为![]() .
.
(1)若关于![]() 的方程
的方程![]() 的两个实数根为
的两个实数根为![]() ,求证:
,求证:![]() ;
;
(2)当![]() 时,证明函数
时,证明函数![]() 在函数
在函数![]() 的最小零点
的最小零点![]() 处取得极小值.
处取得极小值.
【答案】(1)见解析;(2)见解析.
【解析】分析:(1)本小问的解决方法是利用![]() 这个条件,得到含有
这个条件,得到含有![]() 的等式,对等式进行变形处理,使得等式左边是
的等式,对等式进行变形处理,使得等式左边是![]() ,右边是分式
,右边是分式![]() 。则求证目标不等式等价于证等式右端的部分
。则求证目标不等式等价于证等式右端的部分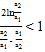 ,运用作差比较法构造函数
,运用作差比较法构造函数![]() ,对
,对![]() 运用导数进行研究,即可证明原不等式;
运用导数进行研究,即可证明原不等式;
(3)讨论函数的单调性,取绝对值得到![]() 的分段形式,若证明
的分段形式,若证明![]() ,则证明
,则证明![]() ,记
,记![]() ,求导分析单调性即可证得.
,求导分析单调性即可证得.
详解:(1)![]() ,由
,由![]() ,
,
得![]() ;由
;由![]() ,得
,得![]() ;
;
所以,![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ,
,
所以![]() ,
,
不妨设![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴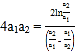 ,
,
设![]() ,则
,则![]() ,
,
所以,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,则
,则![]() ,
,
因![]() ,故
,故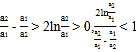 ,所以
,所以![]() ;
;
(2)由(1)可知,![]() 在区间
在区间![]() 单调递增,又
单调递增,又![]() 时,
时,![]() ,
,
易知,![]() 在
在![]() 递增,
递增,![]() ,
,
∴![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
当![]() 时,
时,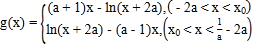 ,
,
于是![]() 时,
时,![]() ,
,
所以,若证明![]() ,则证明
,则证明![]() ,
,
记![]() ,
,
则![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 内单调递增,∴
内单调递增,∴![]() ,
,
∵![]() ,
,
∴![]() 在
在![]() 内单调递增,
内单调递增,
∴![]() ,
,
于是![]() 时,
时,![]() .
.
所以![]() 在
在![]() 递减.
递减.
当![]() 时,相应的
时,相应的![]() .
.
所以![]() 在
在![]() 递增.
递增.
故![]() 是
是![]() 的极小值点.
的极小值点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



