题目内容
在平面直角坐标系中，集合C={（x，y）|y=x}表示直线y=x上的所有点，从这个角度看，若有集合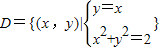
，则集合C、D之间有什么关系？（ ）A．C⊆D
B．D⊆C
C．C∈D
D．D∈C
【答案】分析：集合C={（x，y）|y=x}表示直线y=x上的所有点，解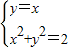
，得
，
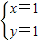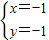，即集合D表示点（1，1）和（-1，-1），根据点的分布确定集合的关系．
解答：解：∵解方程组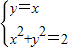
，得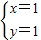
，
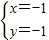
∴集合D表示点（1，1）和（-1，-1）
∵集合C={（x，y）|y=x}表示直线y=x上的所有点，而且点（1，1）和（-1，-1）在直线y=x上，
∴D⊆C
故选B．
点评：本题考查集合的相互关系，属于基本题．
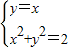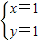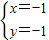，得，，即集合D表示点（1，1）和（-1，-1），根据点的分布确定集合的关系．解答：解：∵解方程组
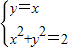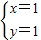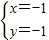
，得，∴集合D表示点（1，1）和（-1，-1）
∵集合C={（x，y）|y=x}表示直线y=x上的所有点，而且点（1，1）和（-1，-1）在直线y=x上，
∴D⊆C
故选B．
点评：本题考查集合的相互关系，属于基本题．
练习册系列答案
相关题目