题目内容
对于已知的x,y,记f(x,y)=min{27-x,27x-y,27y-1},当x∈(0,1),y∈(0,1)时,f(x,y)的最大值为 .
【答案】分析:花括号内给出的三个数的底数相同,以指数为突破口,先由-x小于等于x-y,且-x小于等于y-1求出x的范围,并求出最小值27-x的最大值,然后讨论当0<x< 时,不论另外两个数哪一个最小,其最大值不会超过
时,不论另外两个数哪一个最小,其最大值不会超过 .
.
解答:解:若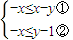 ,由①得y≤2x,由②得y≥1-x,此时1-x≤2x,所以x
,由①得y≤2x,由②得y≥1-x,此时1-x≤2x,所以x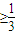 .
.
此时f(x,y)=min{27-x,27x-y,27y-1}=27-x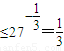 ,
,
当0<x< 时,若y-1<x-y,则y<
时,若y-1<x-y,则y<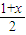 ,y-1<
,y-1<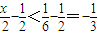 ,此时
,此时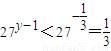 ,
,
若x-y<y-1,则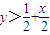 ,x-y<
,x-y<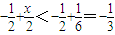 ,此时
,此时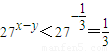 .
.
综上,f(x,y)的最大值为 .
.
故答案为 .
.
点评:本题综合考查了运用函数思想解决问题的能力,考查了函数的值域,该题运用抽象思维能力较强,属中高档题.
 时,不论另外两个数哪一个最小,其最大值不会超过
时,不论另外两个数哪一个最小,其最大值不会超过 .
.解答:解:若
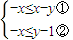 ,由①得y≤2x,由②得y≥1-x,此时1-x≤2x,所以x
,由①得y≤2x,由②得y≥1-x,此时1-x≤2x,所以x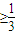 .
.此时f(x,y)=min{27-x,27x-y,27y-1}=27-x
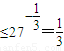 ,
,当0<x<
 时,若y-1<x-y,则y<
时,若y-1<x-y,则y<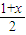 ,y-1<
,y-1<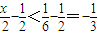 ,此时
,此时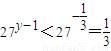 ,
,若x-y<y-1,则
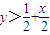 ,x-y<
,x-y<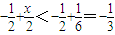 ,此时
,此时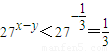 .
.综上,f(x,y)的最大值为
 .
.故答案为
 .
.点评:本题综合考查了运用函数思想解决问题的能力,考查了函数的值域,该题运用抽象思维能力较强,属中高档题.

练习册系列答案
相关题目