Question

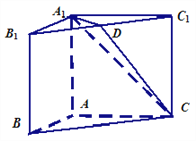
【题目】如图，在三棱柱中，侧面，均为正方形，,点是棱的中点.请建立适当的坐标系，求解下列问题：

（Ⅰ）求证：异面直线与互相垂直；

（Ⅱ）求二面角（钝角）的余弦值.

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ）.

【解析】试题分析：（Ⅰ）由各面间的垂直关系，可建立以为坐标原点的空间直角坐标系，进一步写出各点的坐标，求出坐标，利用两者数量积为可证异面直线 与互相垂直；（Ⅱ）通过空间向量间的运算，求出平面的法向量，平面，得出平面的法向量为．进一步利用二面角与两平面法向量夹角间的关系求出二面角的余弦值．

试题解析：

证：因为侧面，均为正方形， ，

所以两两互相垂直，如图所示建立直角坐标系

设，则.

（Ⅰ）证明：由上可知：， ，

所以,所以，所以，异面直线与互相垂直.

（Ⅱ）解： ，

设平面的法向量为，则有

，， ，

取，得

又因为平面，所以平面的法向量为，分

因为二面角是钝角，所以，二面角的余弦值为.