题目内容
如图,三棱柱ABC-A1B1C1的底面是边长为3的正三角形,侧棱AA1垂直于底面ABC,AA1=
,D是CB延长线上一点,且BD=BC.
(1)求证:直线BC1∥平面AB1D;
(2)求二面角B1-AD-B的大小;
(3)求三棱锥C1-ABB1的体积.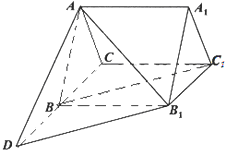
3
| ||
| 2 |
(1)求证:直线BC1∥平面AB1D;
(2)求二面角B1-AD-B的大小;
(3)求三棱锥C1-ABB1的体积.

(1)∵CB∥C1B1,且BD=BC=B1C1,
∴四边形BDB1C1是平行四边形,可得BC1∥DB1.
又B1D?平面AB1D,BC1?平面AB1D,
∴直线BC1∥平面AB1D
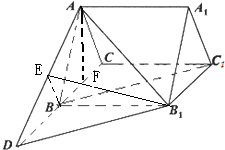
(2)过B作BE⊥AD于E,连接EB1
∵BB1⊥平面ABD,∴BE是B1E在平面ABD内的射影
结合BE⊥AD,可得B1E⊥AD,
∴∠B1EB是二面角B1-AD-B的平面角.
∵BD=BC=AB,
∴E是AD的中点,得BE是三角形ACD的中位线,所以BE=
AC=
.
在Rt△BB1E中,tan∠B1BE=
=
=
∴∠B1EB=60°,即二面角B1-AD-B的大小为60°
(3)过A作AF⊥BC于F,
∵BB1⊥平面ABC,BB1?平面BB1C1C
∴平面BB1C1C⊥平面ABC
∵AF⊥BC,平面BB1C1C∩平面ABC=BC
∴AF⊥平面BB1C1C,即AF为点A到平面BB1C1C的距离.
∵正三角形ABC中,AF=
×3=
,
∴三棱锥C1-ABB1的体积VC1-ABB1=VA-C1BB1=
×
×
=
.
∴四边形BDB1C1是平行四边形,可得BC1∥DB1.
又B1D?平面AB1D,BC1?平面AB1D,

∴直线BC1∥平面AB1D
(2)过B作BE⊥AD于E,连接EB1
∵BB1⊥平面ABD,∴BE是B1E在平面ABD内的射影
结合BE⊥AD,可得B1E⊥AD,
∴∠B1EB是二面角B1-AD-B的平面角.
∵BD=BC=AB,
∴E是AD的中点,得BE是三角形ACD的中位线,所以BE=
| 1 |
| 2 |
| 3 |
| 2 |
在Rt△BB1E中,tan∠B1BE=
| B1B |
| BE |
| ||||
|
| 3 |
∴∠B1EB=60°,即二面角B1-AD-B的大小为60°
(3)过A作AF⊥BC于F,
∵BB1⊥平面ABC,BB1?平面BB1C1C
∴平面BB1C1C⊥平面ABC
∵AF⊥BC,平面BB1C1C∩平面ABC=BC
∴AF⊥平面BB1C1C,即AF为点A到平面BB1C1C的距离.
∵正三角形ABC中,AF=
| ||
| 2 |
3
| ||
| 2 |
∴三棱锥C1-ABB1的体积VC1-ABB1=VA-C1BB1=
| 1 |
| 3 |
9
| ||
| 4 |
3
| ||
| 2 |
| 27 |
| 8 |

练习册系列答案
相关题目

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=