题目内容
如图，设P是圆x2＋y2＝2上的动点，点D是P在x轴上的投影，M为线段PD上一点，且|PD|＝
|MD|．点A(0，
)、F1(－1，0)．
(1)设在x轴上存在定点F2，使|MF1|＋|MF2|为定值，试求F2的坐标，并指出定值是多少？
(2)求|MA|＋|MF1|的最大值，并求此时点M的坐标．
答案：
解析：
解析：
|
(1)设点M的坐标是 因为点Ｄ是Ｐ在 ∵ 即M轨迹是以 由椭圆的定义可知， (2)由(1)知， 当 直线 其中 即所求的
|
，P的坐标是
轴上投影，
为PD上一点，由条件得：
，且
在圆
上，∴
，整理得
，
为焦点的椭圆
三点共线，且
在
延长线上时，取等号．
，联立
，
，解得
的坐标是
．
练习册系列答案
名校课堂系列答案
相关题目
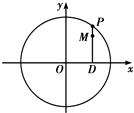如图，设P是圆x2+y2=25上的动点，点D是P在x轴上的射影，M为PD上一点，且|MD|=
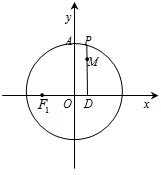如图，设P是圆x2+y2=2上的动点，点D是P在x轴上的投影，M为线段PD上一点，|PD|=
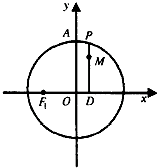如图，设P是圆x2+y2=2上的动点，PD⊥x轴，垂足为D，M为线段PD上一点，且|PD|=
（2012•茂名一模）如图，设P是圆x2+y2=2上的动点，点D是P在x轴上的投影．M为线段PD上一点，且