题目内容
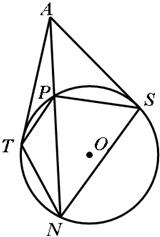
过圆O外一点A作圆O的两条切线AT、AS，切点分别为T、S，过点A作圆O的割线APN，证明：| AT2 |
| AN2 |
| PT•PS |
| NT•NS |
分析：由题意过圆O外一点A作圆O的两条切线AT、AS，切点分别为T、S，过点A作圆O的割线APN，只要证明△ATN∽△APT和△ASN∽△APS，利用比例关系即可证明；
解答：证明：∵AT为圆O的切线，
∴∠ATP=∠ANT，∵∠APN=∠PTN+∠ANT，∠ATN=∠ATP+∠PTN，
∴∠ATN=∠APT，∴△ATN∽△APT，…3分
∴
=
=
，…4分
∴同理可得△ASN∽△APS，
∴
=
=
，…6分
∴
=
=
=
；…8分
故
=
…10分
∴∠ATP=∠ANT，∵∠APN=∠PTN+∠ANT，∠ATN=∠ATP+∠PTN，
∴∠ATN=∠APT，∴△ATN∽△APT，…3分
∴
| AT |
| AP |
| AN |
| AT |
| TN |
| PT |
∴同理可得△ASN∽△APS，
∴
| AS |
| AP |
| AN |
| AS |
| SN |
| PS |
∴
| TN•SN |
| PT•PS |
| AT•AS |
| AP2 |
| AT2 | ||
|
| AN2 |
| AT2 |
故
| AT2 |
| AN2 |
| PT•PS |
| NT•NS |
点评：本题考查的知识点是与圆相关的比例线段，弦切角定理，三角形相似的判断和性质，熟练掌握相似三角形的判断和性质，是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
选做题A．平面几何选讲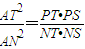
．
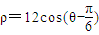上的动点，试求线段AB长的最大值．D．不等式选讲
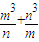≥m2+n2．
．
．