题目内容
17.求函数y=($\frac{1}{2}$)x2+2x的值域.分析 设t=x2+2x,利用换元法结合复合函数单调性之间的关系进行求解即可.
解答 解:设t=x2+2x,则t=(x+1)2-1,
对称轴为x=1,且t=(x+1)2-1≥-1,
则y=($\frac{1}{2}$)t为减函数,
则y=($\frac{1}{2}$)t≤($\frac{1}{2}$)-1=2,
∵y=($\frac{1}{2}$)t>0,
∴0<y≤2,
即函数的值域为(0,2].
点评 本题主要考查函数值域的求解,利用换元法结合复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
7.在直三棱柱ABC-A1B1C1中,AB+BC=4.BB1=3,∠ABC=90°.当三棱柱ABC-A1B1C1的体积最大时.其外接球球的表面积为( )
| A. | $\frac{17\sqrt{17}}{6}π$ | B. | 17π | C. | $\frac{17π}{2}$ | D. | $\frac{17π}{4}$ |
12.若抛物线y=ax2的焦点在直线3x-4y-12=0上,则a等于( )
| A. | -12 | B. | -$\frac{1}{12}$ | C. | -$\frac{1}{6}$ | D. | $\frac{1}{16}$ |
5.观察下面的几何体,哪些是棱柱( )


| A. | ①③⑤ | B. | ①⑥ | C. | ①③⑥ | D. | ③④⑥ |
 .
. 在点
在点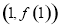 处的切线方程为
处的切线方程为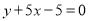 ,求函数
,求函数 是函数
是函数 ,求
,求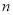 的值;
的值; 时,函数
时,函数 ,且
,且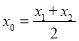 ,求证:
,求证: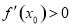 .
. 在区间
在区间 上是增函数,则
上是增函数,则 .
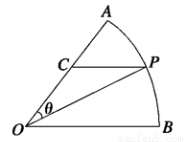
. ,圆心角
,圆心角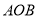 的大小等于
的大小等于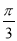 ,半径为
,半径为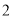 百米,在半径
百米,在半径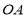 上取一点
上取一点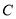 ,过点
,过点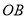 的直线交弧
的直线交弧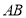 于点
于点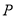 .设
.设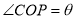 .
.
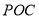 面积
面积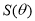 的函数表达式.
的函数表达式.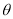 的值.
的值.