Question

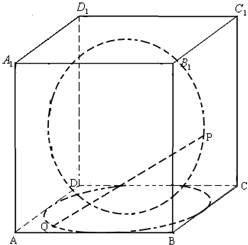如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，P为过正方体表面正方形ABCD，BCC₁B₁，A₁B₁C₁D₁，A₁D₁DA的中心的圆上的一动点，Q为正方形ABCD的内切圆上的一动点，则PQ的最大值与最小值之和为（　　）

• A．

  5 +1

  2

• B．

  3 +1

  2

• C．2
• D．

  2

Answer 1

分析：根据题意，类比平面几何点圆的位置关系，可得当Q是AD中点时，连接OQ，分别交圆O于E，F，则EQ为PQ的最小值，FQ为PQ的最大值，从而得解．

解答：解：由题意，设正方体表面正方形ABCD，BCC₁B₁，A₁B₁C₁D₁，A₁D₁DA的中心的圆的圆心为O，
当Q是AD中点时，连接OQ，分别交圆O于E，F，则EQ为PQ的最小值，FQ为PQ的最大值
此时，EQ=

2

2

-

1

2

，FQ=

2

2

+

1

2

∴PQ的最大值与最小值之和为

2

故选D．

点评：本题以正方体为载体，考查正方体与圆的位置关系，考查距离问题，需要一定的空间想象能力与理解力．