题目内容
如图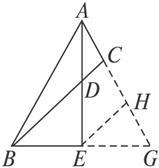
图
证明:延长AC交BE延长线于G.
过E作EH∥BC交AG 于H.则△ABE≌△AGE.
∴EB=EG,AB=AG.
在△GCB中,∵EH∥BC,EB=EG,∴CG=2CH.
∵AB=
∴AG=
在△AEH中,∵DC∥EH,AC=CH,
∴AD=DE.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
如图
图
证明:延长AC交BE延长线于G.
过E作EH∥BC交AG 于H.则△ABE≌△AGE.
∴EB=EG,AB=AG.
在△GCB中,∵EH∥BC,EB=EG,∴CG=2CH.
∵AB=
∴AG=
在△AEH中,∵DC∥EH,AC=CH,
∴AD=DE.
阅读快车系列答案
与
的中点,弦DE交AB、AC于F、G.求证:AF =AG.
