题目内容
【题目】已知数列![]() 满足
满足![]() 且
且![]() ,设
,设![]() ,
,![]() .
.
(1)求![]() ;
;
(2)求![]() 的通项公式;
的通项公式;
(3)求 .
.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)依次代入计算,可求得![]() ;
;
(2)归纳出![]() ,并用数学归纳法证明;
,并用数学归纳法证明;
(3)用裂项相消法求和![]() ,然后求极限.
,然后求极限.
(1)∵![]() 且
且![]() ,
,
∴![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
∴![]() ;
;
(2)由(1)归纳:![]() ,
,
下面用数学归纳法证明:
1°n=1,n=2时,由(1)知成立,
2°假设n=k(k>1)时,结论成立,即bk=2k2,
则n=k+1时,ak=bk-k=2k2-k,![]() ,
,
ak+1=(2k+1)(k+1),
∴bk+1=ak+1+(k+1)=(2k+1)(k+1)+(k+1)=2(k+1)2,
∴n=k+1时结论成立,
∴对所有正整数n,bn=2n2.
(3)由(2)知n![]() 2时,
2时,![]() ,
,
∴![]()
![]()
![]() ,
,
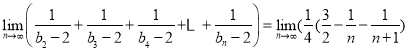
![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目