题目内容
下列四个命题中,假命题是( )A.存在这样的α和β,使得cos(α+β)=cosα·cosβ+sinα·sinβ
B.不存在无穷多个α和β,使得cos(α+β)=cosα·cosβ+sinα·sinβ
C.对任意的α和β,都有cos(α+β)=cosα·cosβ-sinα·sinβ
D.不存在这样的α和β,使得cos(α+β)≠cosα·cosβ-sinα·sinβ
解析:显然C是真命题,它是两角和余弦公式,是恒等式.
由A项命题cos(α+β)=cosα·cosβ+sinαsinβ和公式cos(α+β)=cosα·cosβ-sinα·sinβ得sinα·sinβ=0,显然适合sinα·sinβ=0的α,β存在,即α=nπ(n∈Z)或β=kπ(k∈Z),所以A为真命题;排除了C、D、A得出B是假命题,事实上,对任何α=nπ(n∈Z),或β=kπ(k∈Z)都有cos(α+β)=cosα·cosβ+sinα·sinβ.
答案:B

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,有下列四个命
,有下列四个命 ; B.在所有
; B.在所有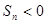 中,
中, 最大;
最大;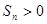 的
的 的个数有11个; D.
的个数有11个; D. ;
;