题目内容
已知 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,有下列四个命
,有下列四个命
题,假命题的是( )
A.公差 ; B.在所有
; B.在所有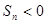 中,
中, 最大;
最大;
C.满足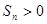 的
的 的个数有11个; D.
的个数有11个; D. ;
;
【答案】
C
【解析】
试题分析:等差数列的前n项和公式 ,
,
所以 ,
,
由 得
得 ,
,
由 ,得
,得 ,
, ,
,

分析A.由 ,可知d<0,正确;
,可知d<0,正确;
分析D.由 得
得 ,又
,又 ,所以
,所以 ,正确;
,正确;
分析C. 满足 的
的 的个数有11个;是假命题。
的个数有11个;是假命题。
因为 >-11×5.5d+55d>0,
>-11×5.5d+55d>0, >-12×5.5d+66d=0,
>-12×5.5d+66d=0,
故选C。
考点:本题主要考查等差数列的通项公式、前n项求和公式,不等式性质。
点评:典型题,等差数列相关知识,是高考考查的重点,本题较全面地考查了等差数列的通
项公式、前n项求和公式,不等式性质等,为中档题。

练习册系列答案
相关题目
 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,
, ,则下列结论错误的是 ( )
,则下列结论错误的是 ( ) 和
和 均为
均为 的最大值. B.
的最大值. B. ;
; ; D.
; D. ;
; 是等差数列
是等差数列 的前n项和,且
的前n项和,且 的值为 ( )
的值为 ( ) 是等差数列
是等差数列 的前n项和,且
的前n项和,且 的值为
的值为 是等差数列
是等差数列 的前n项和,且
的前n项和,且 的值为 ( )
的值为 ( ) 是等差数列
是等差数列 的前n项和,且
的前n项和,且 的值为 (
)
的值为 (
)