题目内容
 如图,连接△ABC的各边中点得到一个新的△A1B1C1,又△A1B1C1的各边中点得到一个新的△A2B2C2,如此无限继续下去,得到一系列三角形,△A1B1C1,△A2B2C2,△A3B3C3,…这一系列三角形趋向于一个点M.已知A(0,0),B(3,0),C(2,2),则点M的坐标是( )
如图,连接△ABC的各边中点得到一个新的△A1B1C1,又△A1B1C1的各边中点得到一个新的△A2B2C2,如此无限继续下去,得到一系列三角形,△A1B1C1,△A2B2C2,△A3B3C3,…这一系列三角形趋向于一个点M.已知A(0,0),B(3,0),C(2,2),则点M的坐标是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(1,
|
分析:根据题意,△ABC的重心坐标为:(
,
),△A1B1C1的重心坐标为:(
,
),再由中点公式得,△A1B1C1的重心坐标也是:(
,
),同理,△A2B2C2的重心坐标也是:(
,
),代入数据可得答案.
| xA+xB+XC |
| 3 |
| YA+YB+YC |
| 3 |
| X1+X2+X3 |
| 3 |
| Y1+Y2+Y3 |
| 3 |
| xA+xB+XC |
| 3 |
| YA+YB+YC |
| 3 |
| xA+xB+XC |
| 3 |
| YA+YB+YC |
| 3 |
解答:解:如图,连接△ABC的各边中点得到一个新的△A1B1C1,
又连接△A1B1C1的各边中点得到△A2B2C2,如此无限继续下去,得到一系列三角形:△ABC,△A1B1C1,△A2B2C2,
因为这一系列三角形重心相同,趋向于一个点M,则点M是△ABC的重心,
已知A(0,0),B(3,0),C(2,2),
∴M=(
,
)
故选A
又连接△A1B1C1的各边中点得到△A2B2C2,如此无限继续下去,得到一系列三角形:△ABC,△A1B1C1,△A2B2C2,
因为这一系列三角形重心相同,趋向于一个点M,则点M是△ABC的重心,
已知A(0,0),B(3,0),C(2,2),
∴M=(
| 5 |
| 3 |
| 2 |
| 3 |
故选A
点评:本题采取了归纳推理的思想得出了点M是△ABC的重心,应用中点坐标公式及三角形重心坐标公式作了简单证明,并用公式求出了点M的坐标.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
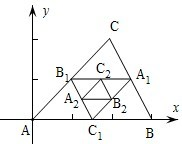 如图,连接△ABC的各边中点得到一个新的△A1B1C1,又连接△A1B1C1的各边中点得到△A2B2C2,如此无限继续下去,得到一系列三角形:△ABC,△A1B1C1,△A2B2C2,…,这一系列三角形趋向于一个点M.已知A(0,0),B(3,0),C(2,2),则点M的坐标是
如图,连接△ABC的各边中点得到一个新的△A1B1C1,又连接△A1B1C1的各边中点得到△A2B2C2,如此无限继续下去,得到一系列三角形:△ABC,△A1B1C1,△A2B2C2,…,这一系列三角形趋向于一个点M.已知A(0,0),B(3,0),C(2,2),则点M的坐标是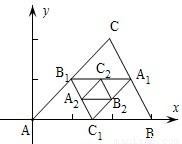

 ,
, )
) ,1)
,1) ,1)
,1) )
)
 ,
, )
) ,1)
,1) ,1)
,1) )
)