题目内容
(理科)已知直线l的方向向量为(-1,0,1),平面α的法向量为(2,-2,1),那么直线l与平面α所成角的大小为________.(用反三角表示)
arcsin
分析:直接利用直线与平面所成的角的向量计算公式(cos< ,
, >=
>= ,其中
,其中 为直线的方向向量,
为直线的方向向量, 为平面α的法向量)求出<
为平面α的法向量)求出< ,
, >,再根据cos<
>,再根据cos< ,
, >的正负即可求出直线l与平面α所成的角.
>的正负即可求出直线l与平面α所成的角.
解答:设直线l的方向向量为 =(-1,0,1),平面α的法向量为
=(-1,0,1),平面α的法向量为 =(2,-2,1)
=(2,-2,1)
∴cos< ,
, >=
>= =
= =-
=- <0
<0
∴直线l与平面α所成角β=< ,
, >-
>-
∴sinβ=-cos< ,
, >=
>=
∴β=arcsin 即直线l与平面α所成角arcsin
即直线l与平面α所成角arcsin
故答案为arcsin
点评:本题主要考查了利用空间向量求直线与平面的夹角.解题的关键是要要熟记直线与平面所成的角的向量计算公式(cos< ,
, >=
>= ,其中
,其中 为直线的方向向量,
为直线的方向向量, 为平面α的法向量)但要注意的是直线与平面所成的角与cos<
为平面α的法向量)但要注意的是直线与平面所成的角与cos< ,
, >的正负有关(若cos<
>的正负有关(若cos< ,
, >>0则直线与平面所成的角为
>>0则直线与平面所成的角为 -<
-< ,
, >,若cos<
>,若cos< ,
, ><0则直线与平面所成的角为<
><0则直线与平面所成的角为< ,
, >-
>- !
!

分析:直接利用直线与平面所成的角的向量计算公式(cos<
 ,
, >=
>= ,其中
,其中 为直线的方向向量,
为直线的方向向量, 为平面α的法向量)求出<
为平面α的法向量)求出< ,
, >,再根据cos<
>,再根据cos< ,
, >的正负即可求出直线l与平面α所成的角.
>的正负即可求出直线l与平面α所成的角.解答:设直线l的方向向量为
 =(-1,0,1),平面α的法向量为
=(-1,0,1),平面α的法向量为 =(2,-2,1)
=(2,-2,1)∴cos<
 ,
, >=
>= =
= =-
=- <0
<0∴直线l与平面α所成角β=<
 ,
, >-
>-
∴sinβ=-cos<
 ,
, >=
>=
∴β=arcsin
 即直线l与平面α所成角arcsin
即直线l与平面α所成角arcsin
故答案为arcsin

点评:本题主要考查了利用空间向量求直线与平面的夹角.解题的关键是要要熟记直线与平面所成的角的向量计算公式(cos<
 ,
, >=
>= ,其中
,其中 为直线的方向向量,
为直线的方向向量, 为平面α的法向量)但要注意的是直线与平面所成的角与cos<
为平面α的法向量)但要注意的是直线与平面所成的角与cos< ,
, >的正负有关(若cos<
>的正负有关(若cos< ,
, >>0则直线与平面所成的角为
>>0则直线与平面所成的角为 -<
-< ,
, >,若cos<
>,若cos< ,
, ><0则直线与平面所成的角为<
><0则直线与平面所成的角为< ,
, >-
>- !
! 
练习册系列答案
相关题目
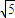 )且方向向量为
)且方向向量为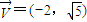 的直线l交椭圆C于A、B两点,交x轴于M点,又
的直线l交椭圆C于A、B两点,交x轴于M点,又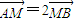 .
.