题目内容
直线l1,l2,l3,…依次为函数y=2sinxcosx+
cos2x图象在y轴右侧从左到右的对称轴,则直线l4的方程为( )
| 3 |
分析:首先利用二倍角的正弦和两角和与差的正弦公式得出y=2sinxcosx+
cos2x=2sin(2x+
),然后求出函数的对称轴集合即可得出答案.
| 3 |
| π |
| 3 |
解答:解:∵y=2sinxcosx+
cos2x=2sin(2x+
)
令2x+
=kπ+
(k∈Z),得x=
+
,
∴y=2sinxcosx+
cos2x的对称轴方程为x=
+
∴当k=4时,对称轴方程为x=
故选D
| 3 |
| π |
| 3 |
令2x+
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 12 |
∴y=2sinxcosx+
| 3 |
| kπ |
| 2 |
| π |
| 12 |
∴当k=4时,对称轴方程为x=
| 25π |
| 12 |
故选D
点评:本题主要考查了二倍角的正弦和余弦、正弦函数的对称性以及三角函数恒等变换等基础知识,属于基础题.

练习册系列答案
相关题目
若图中直线l1,l2,l3的斜率分别为k1,k2,k3,则( )


| A、k1<k2<k3 | B、k1<k3<k2 | C、k3<k2<k1 | D、k3<k1<k2 |
已知向量
,
,
分别是空间三条不同直线l1,l2,l3的方向向量,则下列命题中正确的是( )
| v1 |
| v2 |
| v3 |
A、l1⊥l2,l2⊥
| ||||||
B、l1⊥l2,l 2∥
| ||||||
C、l1,l2,l3平行于同一个平面??λ,μ∈R,使得
| ||||||
D、l1,l2,l3共点??λ,μ∈R,使得
|
 若图中直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
若图中直线l1,l2,l3的斜率分别为k1,k2,k3,则( ) 若图中的直线l1,l2,l3的斜率为k1,k2,k3则( )
若图中的直线l1,l2,l3的斜率为k1,k2,k3则( )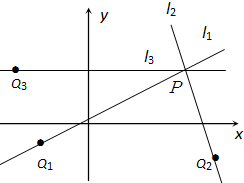 如图,直线l1,l2,l3,都经过点P(3,2),又l1,l2,l3分别经过点Q1(-2,-1),Q2(4,-2),Q3(-3,2),试计算直线l1,l2,l3的斜率.
如图,直线l1,l2,l3,都经过点P(3,2),又l1,l2,l3分别经过点Q1(-2,-1),Q2(4,-2),Q3(-3,2),试计算直线l1,l2,l3的斜率.