题目内容
已知向量 =(4,-2),
=(4,-2), =(cosα,sinα),且
=(cosα,sinα),且 ,则tan2α=
,则tan2α=
- A.

- B.

- C.

- D.

A
分析:利用两个向量的数量积公式,两个向量垂直的性质,可得4cosα-2sinα=0,即tanα=2,利用二倍角公式求得
tan2α 的值.
解答:∵向量 =(4,-2),
=(4,-2), =(cosα,sinα),且
=(cosα,sinα),且 ,则
,则 =4cosα-2sinα=0,
=4cosα-2sinα=0,
∴sinα=2cosα,∴tanα=2,∴tan2α=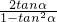 =-
=- ,
,
故选 A.
点评:本题考查两个向量的数量积公式,两个向量垂直的性质,二倍角的正切公式的应用,求出 tanα 的值,
是解题的关键.
分析:利用两个向量的数量积公式,两个向量垂直的性质,可得4cosα-2sinα=0,即tanα=2,利用二倍角公式求得
tan2α 的值.
解答:∵向量
 =(4,-2),
=(4,-2), =(cosα,sinα),且
=(cosα,sinα),且 ,则
,则 =4cosα-2sinα=0,
=4cosα-2sinα=0,∴sinα=2cosα,∴tanα=2,∴tan2α=
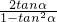 =-
=- ,
,故选 A.
点评:本题考查两个向量的数量积公式,两个向量垂直的性质,二倍角的正切公式的应用,求出 tanα 的值,
是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知向量
=(4,2),
=(6,y),且
∥
,则y等于( )
| a |
| b |
| a |
| b |
| A、3 | B、-3 | C、12 | D、-12 |
已知向量
=(4,2),
=(x,3)向量,且
∥
,则x=( )
| a |
| b |
| a |
| b |
| A、1 | B、5 | C、6 | D、9 |