题目内容
设0<a<1,根据函数的单调性定义证明函数f(x)=lognx+logxa在(1,| 1 | a |
分析:步骤:(1)设元x1、x2,设1<x1<x2<
,
(2)作差:f(x1)-f(x2)=
+
-
-
(3)变形,应用对数运算性质,所有的对数式化为同底的,提取公因式,将式子变成因式乘积的形式,
(4)判断符号(正、负),得出结论.
| 1 |
| a |
(2)作差:f(x1)-f(x2)=
| log | x1 a |
| log | a x1 |
| log | x2 a |
| log | a x2 |
(3)变形,应用对数运算性质,所有的对数式化为同底的,提取公因式,将式子变成因式乘积的形式,
(4)判断符号(正、负),得出结论.
解答:解:证明:设1<x1<x2<
,
f(x1)-f(x2)=
+
-
-
=
(1-
)
由条件得:
>0,
又∵-1≤
、
<0,
∴0<
•
<1,
故 f(x1)-f(x2)>0
∴在(1,
)上f(x)是增函数.
| 1 |
| a |
f(x1)-f(x2)=
| log | x1 a |
| log | a x1 |
| log | x2 a |
| log | a x2 |
=
| log |
a |
| 1 | ||||
|
由条件得:
| log |
a |
又∵-1≤
| log | x1 a |
| log | x2 a |
∴0<
| log | x1 a |
| log | x2 a |
故 f(x1)-f(x2)>0
∴在(1,
| 1 |
| a |
点评:本题考查证明函数单调性的方法步骤.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的定义域为( )
的定义域为( )


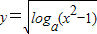 的定义域为( )
的定义域为( )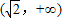
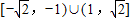
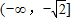
 的定义域为( )
的定义域为( )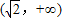


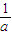 )上是增函数.
)上是增函数.