题目内容

设函数f{x)=|x2-4x-5|，g(x)=k(x-7)．

(1)画出f(x)的简图；

(2)若方程f(x)=g(x)有三个不等实根，求k值的集合；

(3)如果x∈[-1，5]时，函数f(x)的图像总在直线y=k(x-7)的下方，试求出k值的集合．

解：(1)函数简图如下：

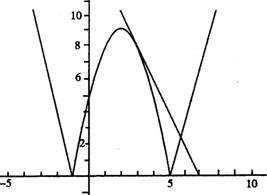
(2)x∈[-1，5]时，f(x)=-x2+4x+5

令-x2+4x+5=k(x-7)，

则x2+(k-4)x-7k-5=0

当△=0时，直线y=k(x-7)与抛物线y=-x2+4x+5 (x∈[-1，5])弧段相切，

由△=(k-4)2+20+28k=0得：

k=-2或k=-18．

当k=-2时，解之，得x=3∈[-1，5]

当k=-18时，x2-22x+121=0．

解之，得x=11[-1，5]

∴A=-2时直线y=k(x-7)与抛物线

y=-x2+4x+5 (x∈[-1，5))弧段相切于点(3，8)

同时，直线y=k(x-7)与抛物线y=x2-4x-5

(x[-1，5])部分相交于不同两点．

由图形可知，直线y=k(x-7)绕点(7，0)转动时，除k=-2外的所有直线与图像无公共点或有两个公共点或有四个公共点．故k=-2为所求．

(3)设k(x-7)＞-x2+4x+5  (x∈[-1，5])恒成立，且k＜=（7-x）+-10

∵7-x＞0，

∴7-x+-10≥-10=-2

∴k＜-2即为所求．

练习册系列答案
相关题目
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
设函数f（x）=p（x-
1
x
）-2lnx，g（x）=
2e
x
（p是实数，e为自然对数的底数）
（1）若f（x）在其定义域内为单调函数，求p的取值范围；
（2）若直线l与函数f（x），g（x）的图象都相切，且与函数f（x）的图象相切于点（1，0），求p的值；
（3）若在[1，e]上至少存在一点x0，使得f（x0）＞g（x0）成立，求p的取值范围．
设函数f（x）的定义域为D，若存在非零实数l使得对于任意x∈M（M⊆D），有x+l∈D，且f（x+1）≥f（x），则称f（x）为M上的高调函数．现给出下列三个命题：
①函数f(x)=(
12
)x为R上的l高调函数；
②函数f（x）=sin2x为R上的π高调函数；
③如果定义域是[-1，+∞）的函数f（x）=x2为[-1，+∞）上的m高调函数，那么实数m的取值范围[2，+∞）；
其中正确的命题是
②③
②③
（填序号）
设函数f（x）是定义在R上的偶函数，且f（x+2）=f（x）恒成立；当x∈[0，1]时，f（x）=x3-4x+3．有下列命题：
①f(-
3
4
) ＜f(
15
2
)；
②当x∈[-1，0]时f（x）=x3+4x+3；
③f（x）（x≥0）的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列；
④关于x的方程f（x）=|x|在x∈[-3，4]上有7个不同的根．
其中真命题的个数为（　　）
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网