题目内容
已知数列ξ中,a1=0,an+1=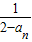 (n∈N*).
(n∈N*).(1)计算a2,a3,a4;
(2)猜想数列{an}的通项公式并用数学归纳法证明.
【答案】分析:(1)依题意,由a1=0,an+1=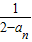 (n∈N*)即可求得a2,a3,a4;
(n∈N*)即可求得a2,a3,a4;
(2)通过(1)可猜想an=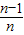 (n=1,2,3,…);下面用数学归纳法证明即可:先证当n=1时结论成立,再假设假设n=k时,结论成立,去证明当n=k+1时,等式也成立即可.
(n=1,2,3,…);下面用数学归纳法证明即可:先证当n=1时结论成立,再假设假设n=k时,结论成立,去证明当n=k+1时,等式也成立即可.
解答:解:(1)a2= ,a3=
,a3=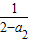 =
= ,同理可得a4=
,同理可得a4= …(3分)
…(3分)
(2)猜想an=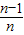 (n=1,2,3,…)…(6分)
(n=1,2,3,…)…(6分)
证明:①当n=1时,结论显然成立…(8分)
②假设n=k时,结论成立,即ak=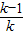 ,
,
那么当n=k+1时,ak+1=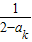 =
=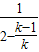 =
=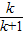 =
=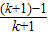 ,
,
即当n=k+1时,等式成立.
由①②知,an=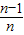 对一切自然数n都成立.…(13分)
对一切自然数n都成立.…(13分)
点评:本题考查数列的递推式,考查归纳猜想,着重考查数学归纳法,考查推理与证明,属于难题.
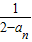 (n∈N*)即可求得a2,a3,a4;
(n∈N*)即可求得a2,a3,a4;(2)通过(1)可猜想an=
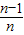 (n=1,2,3,…);下面用数学归纳法证明即可:先证当n=1时结论成立,再假设假设n=k时,结论成立,去证明当n=k+1时,等式也成立即可.
(n=1,2,3,…);下面用数学归纳法证明即可:先证当n=1时结论成立,再假设假设n=k时,结论成立,去证明当n=k+1时,等式也成立即可.解答:解:(1)a2=
 ,a3=
,a3=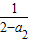 =
= ,同理可得a4=
,同理可得a4= …(3分)
…(3分)(2)猜想an=
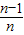 (n=1,2,3,…)…(6分)
(n=1,2,3,…)…(6分)证明:①当n=1时,结论显然成立…(8分)
②假设n=k时,结论成立,即ak=
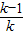 ,
,那么当n=k+1时,ak+1=
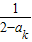 =
=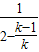 =
=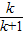 =
=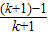 ,
,即当n=k+1时,等式成立.
由①②知,an=
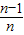 对一切自然数n都成立.…(13分)
对一切自然数n都成立.…(13分)点评:本题考查数列的递推式,考查归纳猜想,着重考查数学归纳法,考查推理与证明,属于难题.

练习册系列答案
相关题目
 13、已知数列{an}中,a1=1,an+1=an+n,利用如图所示的程序可求该数列的第
13、已知数列{an}中,a1=1,an+1=an+n,利用如图所示的程序可求该数列的第