题目内容
已知方程
=k在（0，+∞）上有两个不同的解α，β（α＜β），则下面结论正确的是（ ）
| |sinx| |
| x |
| A、sin2α=2αcos2α |
| B、cos2α=2αsin2α |
| C、sin2β=2βcos2β |
| D、cos2β=2βsin2β |
分析：由题意可得，y=|sin x|的图象与直线y=kx（k＞0）在（0，+∞）上有且仅有两个公共点，故直线y=kx与y=|sin x|在（π，
π）内相切，且切于点（β，-sin β），切线的斜率为-cos β=
，化简可得结论．
| 3 |
| 2 |
| -sinβ |
| β |
解答：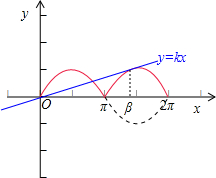
解：∵
=k，∴|sin x|=kx，
∴要使方程
=k（k＞0）在（0，+∞）上有两个不同的解，
则y=|sin x|的图象与直线y=kx（k＞0）在（0，+∞）上
有且仅有两个公共点，
所以直线y=kx与y=|sin x|在（π，
π）内相切，
且切于点（β，-sin β），
∴切线的斜率为-cos β=
，∴βcos β=sin β，
∴sin 2β=2sin βcos β=2βcos2β，
故选：C．
解：∵| |sinx| |
| x |
∴要使方程
| |sinx| |
| x |
则y=|sin x|的图象与直线y=kx（k＞0）在（0，+∞）上
有且仅有两个公共点，
所以直线y=kx与y=|sin x|在（π，
| 3 |
| 2 |
且切于点（β，-sin β），
∴切线的斜率为-cos β=
| -sinβ |
| β |
∴sin 2β=2sin βcos β=2βcos2β，
故选：C．
点评：本题主要考查函数的零点与方程的根的关系，导数的几何意义，体现了转化的数学思想，属于中档题．
练习册系列答案
全优点练单元计划系列答案
相关题目