题目内容
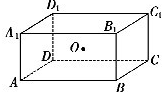 如图,长方体ABCD-A1B1C1D1中,其中AB=a,,AD=b,AA1=c外接球球心为点O,外接球体积为
如图,长方体ABCD-A1B1C1D1中,其中AB=a,,AD=b,AA1=c外接球球心为点O,外接球体积为| 32π |
| 3 |
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| 4 |
分析:考查球面距离的问题,可先利用长方体三边长求出球半径,在三角形中求出球心角,再利用球面距离公式得出答案.
解答:解:设A、B两点在该球面上的球面距离为d,
∵外接球体积为
,∴R=2,
球的直径即为长方体的对角线长,
即2R=
=4,
若
+
的最小值为
,∴a2+b2=4,
在等腰三角形OAC中,OA=OC=AC
球心角∠AOC=
,
∴利用球面距离公式得出:d=α•R=
•2=
故答案为:
.
∵外接球体积为
| 32π |
| 3 |
球的直径即为长方体的对角线长,
即2R=
| a 2+b 2+c 2 |
若
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| 4 |
在等腰三角形OAC中,OA=OC=AC
球心角∠AOC=
| π |
| 3 |
∴利用球面距离公式得出:d=α•R=
| π |
| 3 |
| 2π |
| 3 |
故答案为:
| 2π |
| 3 |
点评:本题主要考查球的性质、球内接多面体、球面距离及基本不等式,属于基础题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 15、如图,长方体ABCD-A1B1C1D1中被截去一部分,
15、如图,长方体ABCD-A1B1C1D1中被截去一部分, 如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中
如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中 如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.
如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.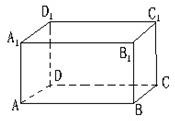 已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )
已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )