题目内容
【题目】已知各项均不相等的等差数列{an}满足a1=1，且a1 ， a2 ， a5成等比数列．
（1）求{an}的通项公式；
（2）若bn=（﹣1）n 
（n∈N*），求数列{bn}的前n项和Sn ．
【答案】
（1）解：设各项均不相等的等差数列{an}的公差为d，满足a1=1，
且a1，a2，a5成等比数列，
可得a22=a1a5，即（1+d）2=1+4d，
解得d=2（0舍去），
则an=1+2（n﹣1）=2n﹣1（n∈N*）
（2）解：bn=（﹣1）n 
=（﹣1）n 
=（﹣1）n（ 
+ 
），
当n为偶数时，前n项和Sn=（﹣1﹣ 
）+（ ﹣ 
）+（﹣ ﹣ 
）+…+（ + ）
=﹣1+ =﹣ 
；
当n为奇数时，n﹣1为偶数，前n项和Sn=Sn﹣1+（﹣ ﹣ ）
=﹣ 
+（﹣ ﹣ ）=﹣ 
．
则Sn=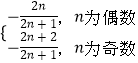 
【解析】（1）设各项均不相等的等差数列{an}的公差为d，由等差数列的通项公式和等比数列中项的性质，解方程可得d=2，进而得到所求通项公式；（2）求得bn=（﹣1）n =（﹣1）n（ + ），再分n为偶数和奇数，运用裂项相消求和，化简整理即可得到所求和．
练习册系列答案
相关题目
