题目内容
已知函数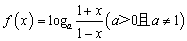 .
.
(1)若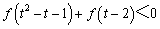 ,求实数
,求实数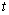 的取值范围;
的取值范围;
(2)若 时,函数
时,函数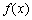 的值域是
的值域是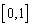 ,求实数
,求实数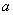 的值.
的值.
解:(1)由已知,函数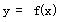 的定义域为
的定义域为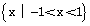 ,
,
因为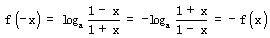 ,
,
所以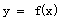 为奇函数,…………………………………………………………… 2分
为奇函数,…………………………………………………………… 2分
设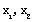 是
是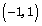 上的任意两个实数,且
上的任意两个实数,且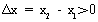 ,
,
则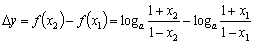 .
.
因为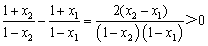 ,
,
所以当a>1时,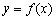 在
在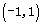 上是增函数;
上是增函数;
当0<a<1时,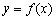 在
在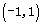 上是减函数. …
上是减函数. …
所以原不等式可化为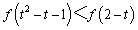 .
.
当a>1时,由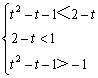 ,得
,得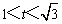 ;…分
;…分
当0<a<1时,由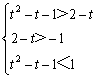 ,得
,得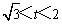 . …
. …
(如果函数的奇偶性和单调性没有证明,但不等式解对扣2分.)
(2)当a>1时,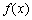 在
在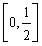 单调递增,则由
单调递增,则由 ,
,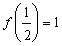 ,
,
得a=3.
当0<a<1时,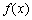 在
在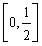 上单调递减,此时
上单调递减,此时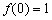 无解.
无解.
综上可知,a=3.

练习册系列答案
相关题目
 }是等差数列,
}是等差数列,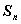 是其前n项和,且
是其前n项和,且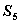 <
<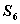 ,
,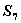 >
>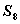 ,则下列说法错误的是
,则下列说法错误的是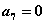 C
C 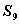 >
> 中,当
中,当
 时,
时,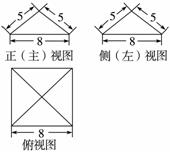
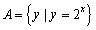 ,集合
,集合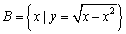 .求
.求 :
: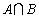 ;
;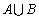 .
.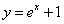 在点A(0,1)处的切线斜率为( )
在点A(0,1)处的切线斜率为( )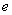 D.
D.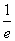
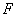 ,虚轴的一个端点为
,虚轴的一个端点为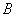 ,如果直线
,如果直线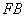 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )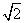 B.
B.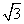 C.
C. D.
D.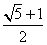
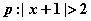 , 条件
, 条件 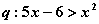 ,则
,则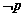 是
是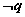 的( )
的( ) 中,若
中,若 ,
, ,则
,则 的值为 ( )
的值为 ( ) B.
B. C.
C. D.
D.