题目内容
(1)已知数列{an}的第1项 a1=1,且an+1=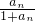 ( n=1,2,3…)使用归纳法归纳出这个数列的通项公式.(不需证明)
( n=1,2,3…)使用归纳法归纳出这个数列的通项公式.(不需证明)
(2)用分析法证明:若a>0,则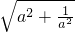 -
- ≥a+
≥a+ -2.
-2.
解:(1)由 a1=1,且an+1=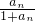 可得,a2=
可得,a2= =
= ,a3=
,a3= =
= ,猜想
,猜想  .
.
(2)证明:要证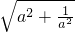 -
- ≥a+
≥a+ -2,只需证
-2,只需证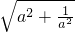 +2≥a+
+2≥a+ +
+ .
.
∵a>0,∴两边均大于零,因此只需证(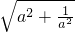 +2)2≥(a+
+2)2≥(a+ +
+ )2,
)2,
只需证a2+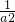 +4+4
+4+4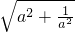 ≥a2+
≥a2+ +2+2
+2+2 (a+
(a+ ),
),
只需证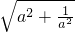 ≥
≥ (a+
(a+ ),只需证a2+
),只需证a2+ ≥
≥ (a2+
(a2+ +2),
+2),
即证a2+ ≥2,它显然是成立,∴原不等式成立.
≥2,它显然是成立,∴原不等式成立.
分析:(1)由 a1=1,且an+1=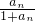 可求得数列的前若干项,根据每项的结构特征猜想通项公式.
可求得数列的前若干项,根据每项的结构特征猜想通项公式.
(2)只需证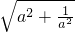 +2≥a+
+2≥a+ +
+ ,只需证(
,只需证(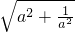 +2)2≥(a+
+2)2≥(a+ +
+ )2,
)2,
只需证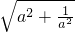 ≥
≥ (a+
(a+ ),即证 a2+
),即证 a2+ ≥2,而它显然是成立.
≥2,而它显然是成立.
点评:本题考查归纳推理,以及用分析法证明不等式,寻找使不等式成立的充分条件,是解题的关键.
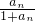 可得,a2=
可得,a2= =
= ,a3=
,a3= =
= ,猜想
,猜想  .
.(2)证明:要证
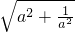 -
- ≥a+
≥a+ -2,只需证
-2,只需证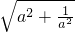 +2≥a+
+2≥a+ +
+ .
.∵a>0,∴两边均大于零,因此只需证(
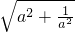 +2)2≥(a+
+2)2≥(a+ +
+ )2,
)2,只需证a2+
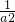 +4+4
+4+4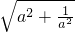 ≥a2+
≥a2+ +2+2
+2+2 (a+
(a+ ),
),只需证
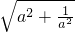 ≥
≥ (a+
(a+ ),只需证a2+
),只需证a2+ ≥
≥ (a2+
(a2+ +2),
+2),即证a2+
 ≥2,它显然是成立,∴原不等式成立.
≥2,它显然是成立,∴原不等式成立.分析:(1)由 a1=1,且an+1=
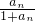 可求得数列的前若干项,根据每项的结构特征猜想通项公式.
可求得数列的前若干项,根据每项的结构特征猜想通项公式.(2)只需证
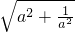 +2≥a+
+2≥a+ +
+ ,只需证(
,只需证(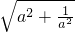 +2)2≥(a+
+2)2≥(a+ +
+ )2,
)2,只需证
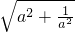 ≥
≥ (a+
(a+ ),即证 a2+
),即证 a2+ ≥2,而它显然是成立.
≥2,而它显然是成立.点评:本题考查归纳推理,以及用分析法证明不等式,寻找使不等式成立的充分条件,是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
(1)已知数列{an}的第1项 a1=1,且an+1=
( n=1,2,3…)使用归纳法归纳出这个数列的通项公式.(不需证明)
(2)用分析法证明:若a>0,则
-
≥a+
-2.
| an |
| 1+an |
(2)用分析法证明:若a>0,则
a2+
|
| 2 |
| 1 |
| a |