题目内容
已知Sn和Tn分别是两个等差数列的前n项和，已知| Sn |
| Tn |
| 7n+2 |
| n+3 |
| a5 |
| b5 |
分析：根据等差数列的性质可知，项数之和相等的两项的和相等得到
=
，把n=9代入
中即可求出比值．
| a5 |
| b5 |
| S9 |
| T9 |
| 7n+2 |
| n+3 |
解答：解：因为Sn和Tn分别是两个等差数列，所以S9=a1+a2+…+a9=5a5；T9=b1+b2+…+b9=5b5．
则
=
=
=
=
故答案为：
则
| S9 |
| T9 |
| 5a5 |
| 5b5 |
| a5 |
| b5 |
| 7×9+2 |
| 9+3 |
| 65 |
| 12 |
故答案为：
| 65 |
| 12 |
点评：此题考查学生掌握等差数列的前n项和的公式，灵活运用等差数列的性质化简求值．
练习册系列答案
相关题目
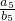，对一切自然数n∈N*成立，则
=________．
，对一切自然数n∈N*成立，则
= ．