题目内容
已知函数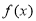 是定义域在
是定义域在 上的不恒为零的函数,且对于任意非零实数
上的不恒为零的函数,且对于任意非零实数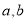 满足
满足 .
.
(1)求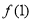 与
与 的值;
的值;
(2)判断并证明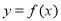 的奇偶性;
的奇偶性;
(3)若函数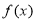 在
在 上单调递减,求不等式
上单调递减,求不等式 的解集.
的解集.
(1) ;(2)偶函数;(3)
;(2)偶函数;(3) .
.
【解析】
试题分析:(1)赋值法求值,令 求得
求得 ,令
,令 求得
求得 ;(2)判断函数奇偶性首先定义域为
;(2)判断函数奇偶性首先定义域为 ,再判断
,再判断 和
和 的关系,显然题干中,没有
的关系,显然题干中,没有 和
和 ,需要赋值令
,需要赋值令 同时结合(1)中
同时结合(1)中 ,代入化简得到
,代入化简得到 ,所以函数
,所以函数 是偶函数;(3)根据(1)(2)
是偶函数;(3)根据(1)(2) ,
, 和定义在
和定义在 的偶函数,且在
的偶函数,且在 单调递减,知
单调递减,知 单调递增,可画出
单调递增,可画出 的图像的简图,不等式
的图像的简图,不等式 化为:
化为: 且
且
进而求得原不等式的解集.
试题解析:(1)

令

 .2分
.2分
令 ,
, 
 .4分
.4分
(2)
 ,令
,令
则
由(1)知


 是偶函数 7分
是偶函数 7分
(3)由(2)知 是偶函数
是偶函数

 ,且
,且 在
在 上单调递减
上单调递减

 在
在 上单调递增.
上单调递增.
 且
且 解得
解得  且
且
 不等式
不等式 的解集为
的解集为 .12分
.12分
考点:1.赋值法求值;2.函数的奇偶性定义;3.数形结合思想.

练习册系列答案
相关题目
 的解集是区间
的解集是区间 的子集,则实数
的子集,则实数 的取值范围为
的取值范围为  的图像恒过定点 .
的图像恒过定点 .  ”是“
”是“ ”的( )
”的( ) ,集合
,集合 ,
, ,
,
 (∁UB),(∁UA)
(∁UB),(∁UA) B;
B; 求
求 的取值范围.
的取值范围. 的图象,则
的图象,则 与
与 的大小关系是 ( )
的大小关系是 ( )

 ,且
,且 ,则实数
,则实数 的值为___ .
的值为___ . : “方程
: “方程 表示双曲线” (
表示双曲线” ( );命题
);命题 :
: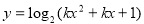 定义域为
定义域为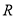 ,若命题
,若命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数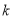 的取值范围.
的取值范围.