Question

 设两球队A， B进行友谊比赛，在每局比赛中A队获胜的概率都是       p（0≤p≤1），

   （Ⅰ）若比赛6局，且p＝，求其中一队至多获胜4局的概率是多少？

   （Ⅱ）若比赛6局，求A队恰好获胜3局的概率的最大值是多少？

   （Ⅲ）若采用“五局三胜”制，求A队获胜时的比赛局数ξ的分布列和数学期望．

 

 

 

 

 

 

 

 

 

 

 

Answer 1

【答案】

 解析：（Ⅰ）设“比赛6局，A队至多获胜4局”为事件A，

则＝1－＝

∴A队至多获胜4局的概率为．                                 （2分）

（Ⅱ）设“若比赛6局，A队恰好获胜3局”为事件B，则．

当p＝0或p＝1时，显然有．

当0＜p＜1时，

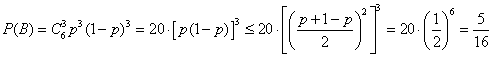
当且仅当p＝1－p，即p＝时取等号 ．

故A队恰好获胜3局的概率的最大值是．                      （6分）

（Ⅲ）若采用“五局三胜”制，A队获胜时的比赛局数ξ＝3，4，5．

，

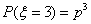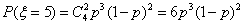，                         （8分）

所以的分布列为：

 

ξ	3	4	5
P

 

 

（10分）

 

E（ξ）＝3p³（10pp＋15） ．                                      （12分）

评析：该题中有个易错点，譬如“5局3胜制”中不是5局中赢得3场即可，而是不一定需要3场比赛，最后一局的胜者一定是获胜者，甚至出现极限情况“三局全胜”不需要再比；