题目内容
函数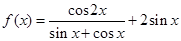 .
.
(Ⅰ)在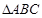 中,
中,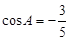 ,求
,求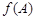 的值;
的值;
(Ⅱ)求函数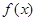 的最小正周期及其图象的所有对称轴的方程.
的最小正周期及其图象的所有对称轴的方程.
【答案】
(Ⅰ)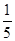 ;(Ⅱ)
;(Ⅱ) ,
,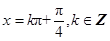
【解析】
试题分析:(Ⅰ)由已知条件可求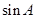 的值。化简函数
的值。化简函数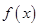 时余弦的二倍角公式有三个,分析可知应用
时余弦的二倍角公式有三个,分析可知应用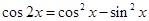 ,然后按平方差公式展开可消去分母将其化简,将
,然后按平方差公式展开可消去分母将其化简,将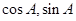 代入化简后的
代入化简后的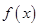 即可求
即可求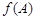 的值;(Ⅱ)用化一公式再将其继续化简为
的值;(Ⅱ)用化一公式再将其继续化简为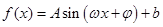 的形式。根据周期公式
的形式。根据周期公式 求周期,再将
求周期,再将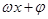 视为整体代入正弦函数对称轴公式
视为整体代入正弦函数对称轴公式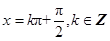 即可得其对称轴方程。
即可得其对称轴方程。
试题解析:解:(Ⅰ)由 得
得 .
.
因为,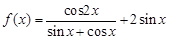
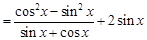 2分
2分
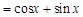
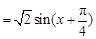 ,
4分
,
4分
因为在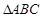 中,
中,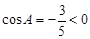 ,
,
所以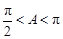 ,
5分
,
5分
所以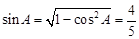 ,
7分
,
7分
所以 .
8分
.
8分
(Ⅱ)由(Ⅰ)可得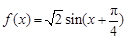 ,
,
所以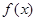 的最小正周期
的最小正周期 .
10分
.
10分
因为函数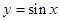 的对称轴为
的对称轴为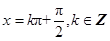 ,
11分
,
11分
又由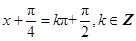 ,得
,得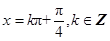 ,
,
所以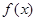 的对称轴的方程为
的对称轴的方程为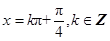 .
13分
.
13分
考点:用二倍角公式、化一公式等化简三角函数,正弦函数的周期及对称轴,考查整体思想及计算能力。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
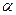 为锐角,且
为锐角,且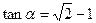 ,函数
,函数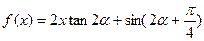 ,数列{
,数列{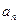 }的首项
}的首项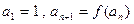 .
. 的表达式;
的表达式;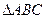 中,若
中,若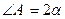 ,
,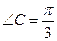 ,BC=2,求
,BC=2,求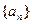 的前
的前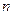 项和
项和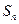 .
. ,其中向量
,其中向量 ,
, ,
, .在
.在 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为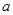 ,
, ,
, .
. 的取值范围及此时函数
的取值范围及此时函数 的值域;
的值域; ,边
,边 ,求
,求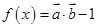 ,其中向量
,其中向量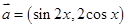 ,
,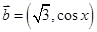 ,
, .在
.在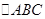 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为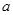 ,
,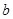 ,
,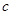 .
.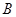 的取值范围及此时函数
的取值范围及此时函数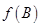 的值域;
的值域;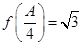 ,
,
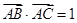 ,求
,求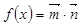 ,其中
,其中 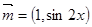 ,
,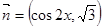 ,在
,在 中,
中,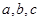 分别是角
分别是角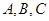 的对边,且
的对边,且 ,
,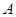 ;(2)若
;(2)若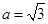 ,
,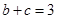 ,求
,求 是定义在
是定义在 上的偶函数,且在
上的偶函数,且在 上是增函数,
上是增函数, ,则
,则 ;
; 中,“
中,“ ”是“
”是“ ”的充要条件;
”的充要条件; 的图象在点
的图象在点 处的切线方程是
处的切线方程是 ,
,
 处取到极大值,
处取到极大值, 的取值范围是(-1,0)
的取值范围是(-1,0)