Question

已知数列{a_n}中,a₁=1,a₂=2,且a_n+1=(1+q)a_n-qa_n-1(n≥2,q≠0).

(1)设b_n=a_n+1-a_n(n∈N^*),证明{b_n}是等比数列;

(2)求数列{a_n}的通项公式;

(3)若a₃是a₆与a₉的等差中项,求q的值,并证明:对任意的n∈N^*,a_n是a_n+3与a_n+6的等差中项.

Answer 1

答案：本小题主要考查等差数列、等比数列的概念、等比数列的通项公式及前n项和公式,考查运算能力和推理论证能力及分类讨论的思想方法.

(1)证明:由题设a_n+1=(1+q)a_n-qa_n-1(n≥2),得

a_n+1-a_n=q(a_n-a_n-1),即b_n=qb_n-1,n≥2.

又b₁=a₂-a₁=1,q≠0,所以{b_n}是首项为1,公比为q的等比数列.

(2)解:由(1),a₂-a₁=1,

a₃-a₂=q,

…

a_n-a_n-1=q^n-2(n≥2).

将以上各式相加,得a_n-a₁=1+q+…+q^n-2(n≥2).

所以当n≥2时,a_n=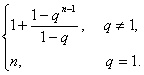

上式对n=1显然成立.

(3)解:由(2),当q=1时,显然a₃不是a₆与a₉的等差中项,故q≠1.

由a₃-a₆=a₉-a₃可得q⁵-q²=q²-q⁸,

由q≠0得q³-1=1-q⁶,                                                            ①

整理得(q³)²+q³-2=0,

解得q³=-2或q³=1(舍去).

于是q=.

另一方面,a_n-a_n+3=,

a_n+6-a_n=

由①可得a_n-a_n+3=a_n+6-a_n,n∈N^*.

所以对任意的n∈N^*,a_n是a_n+3与a_n+6的等差中项.