题目内容
下列命题：
①函数
在
上是减函数；
②点A（1，1）、B（2，7）在直线
两侧；
③数列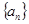
为递减的等差数列，
，设数列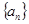的前n项和为
，则当
时，取得最大值；
④定义运算
则函数
的图象在点
处的切线方程是
其中正确命题的序号是
________（把所有正确命题的序号都写上）.
②④
解析试题分析：①函数
，在
上是增函数；②将A,B两点坐标代入方程分别得
，所以两点在直线两侧；③
，又数列递减，所以当
时
最大；④函数
所以切线为
考点：函数单调性，导数几何意义，数列求和及线性规划
点评：本题涉及到的知识点较多，学生在解答时需认真考虑每一项，否则容易发生错选漏选的问题
练习册系列答案
相关题目
在
上是减函数；
两侧；
为递减的等差数列，
，设数列
，则当
时，
则函数
的图象在点
处的切线方程是
________（把所有正确命题的序号都写上）.
在
上是减函数； 
两侧； 
为递减的等差数列，
，设数列
，则当
时，
则函数
的图象在点
处的切线方程是
其中正确命题的序号是 （把所有正确命题的序号都写上）.
在第一象限是增函数；②函数
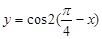是偶函数；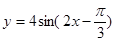 
的一个对称中心是（
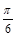，0）；
在闭区间
上是增函数;
在
上是减函数； 
在直线
两侧； 
为递减的等差数列，
，设数列
，则当
时，
， 则函数
的图象在点
处的切线方程是
其中正确命题的序号是_______________（把所有正确命题的序号都写上）．