题目内容
下列命题：
①函数
在
上是减函数；
②点A（1，1）、B（2，7）在直线
两侧；
③数列
为递减的等差数列，
，设数列的前n项和为
，则当
时，取得最大值；
④定义运算
则函数
的图象在点
处的切线方程是
其中正确命题的序号是 （把所有正确命题的序号都写上）.
【答案】
②④
【解析】对①，
，从而可知函数
在
上是增函数，为假命题；对②,由
可知,点A（1，1）、B（2，7）在直线
两侧，为真命题；对③，由
，得
，又数列
单调递减，所以当
或
时，
取得最大值，为假命题；
对④，由定义可知
，故
.则
.所以函数
在点
处的切线方程为
，化为一般式为
，为真命题.
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
在第一象限是增函数；② 函数
的最小正周期是
；
的图像的对称中心是
；
的递减区间是[
；
在
上是减函数；
两侧；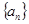
为递减的等差数列，
，设数列
，则当
时，
则函数
的图象在点
处的切线方程是
________（把所有正确命题的序号都写上）.
在其定义域上是增函数；
②函数
是偶函数；
的图象可由
的图象向右平移2个单位得到； 
，则
； 则上述正确命题的序号是
. 
在第一象限是增函数；
是偶函数； 
的一个对称中心是（
，0）；
在闭区间
上是增函数.
在第一象限是增函数；②函数
是偶函数； ③函数
的一个对称中心是（
，0）；④函数
在闭区间
上是增函数; ⑤
是函数
的一条对称轴方程；