题目内容
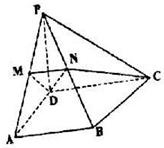在四棱锥P-ABCD中，AD⊥AB，CD∥AB，PD⊥底面ABCD，| AB |
| AD |
| 2 |
（1）求二面角P-MN-D的大小；
（2）当
| CD |
| AB |
分析：（1）由已知中AD⊥AB，CD∥AB，PD⊥底面ABCD，我们可得∠PMD为二面角P-MN-D的平面角．由线PA与底面ABCD成60°角，进而可以得到，△PMD为等腰三角形，∠PMD=120°即二面角P-MN-D的大小；
（2）若，△CDN为直角三角形，则必有CN⊥DN，连BD，设AD=a，我们可以得到Rt△BD∽Rt△CDB，然后根据相似三角形的性质得到
的值．
（2）若，△CDN为直角三角形，则必有CN⊥DN，连BD，设AD=a，我们可以得到Rt△BD∽Rt△CDB，然后根据相似三角形的性质得到
| CD |
| AB |
解答：解：（1）由已知AD⊥AB，PD⊥AB，得AB⊥平面PAD，
又MN∥AB，∴MN⊥平面PAD，MN⊥PM，MN⊥DM
∴∠PMD为二面角P-MN-D的平面角．（3分）
由已知∠PAD=60°，得∠MPD=30°，
∵DM是Rt△PDA斜边PA上的中线，MD=MP
∴△PMD为等腰三角形，∠PMD=120°，
即二面角P-MN-D的大小为120°．（7分）
（2）显然∠DCN≠90°．若∠CDN=90°，则CD⊥平面PAN，
而CD⊥平面PAD，故平面PAN与平面PAD重合，与题意不符．
由△CDN是Rt△，则必有CN⊥DN，
连BD，设AD=a，由已知得AB=
a，从而BD=
a，
又PD=ADtan60°
a，
∴PD=BD，得DN⊥PB，
故DN⊥平面PBC，（10分）
∴DN⊥BC，又PD⊥BC，
∴BC⊥平面PBD，
∴BD⊥BC，反之亦然．
∵AB∥CD
∴∠ABD=∠CDB，
∴Rt△BD∽Rt△CDB（12分）
∴
=
CD=
=
=
．（14分）
又MN∥AB，∴MN⊥平面PAD，MN⊥PM，MN⊥DM
∴∠PMD为二面角P-MN-D的平面角．（3分）
由已知∠PAD=60°，得∠MPD=30°，
∵DM是Rt△PDA斜边PA上的中线，MD=MP
∴△PMD为等腰三角形，∠PMD=120°，
即二面角P-MN-D的大小为120°．（7分）
（2）显然∠DCN≠90°．若∠CDN=90°，则CD⊥平面PAN，
而CD⊥平面PAD，故平面PAN与平面PAD重合，与题意不符．
由△CDN是Rt△，则必有CN⊥DN，
连BD，设AD=a，由已知得AB=
| 2 |
| 3 |
又PD=ADtan60°
| 3 |
∴PD=BD，得DN⊥PB，
故DN⊥平面PBC，（10分）
∴DN⊥BC，又PD⊥BC，
∴BC⊥平面PBD，
∴BD⊥BC，反之亦然．
∵AB∥CD
∴∠ABD=∠CDB，
∴Rt△BD∽Rt△CDB（12分）
∴
| CD |
| BD |
| BD |
| AB |
CD=
| BD2 |
| AB |
| CD |
| AB |
| BD2 |
| AB2 |
| 3 |
| 2 |
点评：本题考查的知识点是二面角的平面角及求法，直线与平面垂直的性质，其中（1）的关键是得到∠PMD为二面角P-MN-D的平面角，而（2）的关键是得到Rt△BD∽Rt△CDB．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
如图，在四棱锥P-ABCD中，底面为直角梯形，AD∥BC，∠BAD=90，PA⊥底面ABCD，且PA=AD=AB=2BC=2，M，N分别为PC、PB的中点．
如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4．AB=2，AN⊥PC于点N，M是PD中点．
如图，在四棱锥P-ABCD中，底面ABCD是矩形，O为底面中心，PA⊥平面ABCD，PA=AD=2AB．M是PD的中点
如图，在四棱锥P-ABCD中，底面ABCD是矩形，已知AB=3，AD=2，PA=2，PD=2
（2009•成都模拟）如图，在四棱锥P-ABCD中，底面ABCD为正方形，且PD⊥平面ABCD，PD=AB=1，EF分别是PB、AD的中点，