题目内容
已知双曲线![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,点
,点![]() ,
,![]() 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.
(1)求直线![]() 与
与![]() 交点的轨迹E的方程
交点的轨迹E的方程
(2)若过点H(0, h)(h>1)的两条直线![]() 和
和![]() 与轨迹E都只有一个交点,且
与轨迹E都只有一个交点,且![]() ,求
,求![]() 的值.
的值.
 [来 经检验,以上所得椭圆的四个顶点无法取到,故交点轨迹E的方程为
[来 经检验,以上所得椭圆的四个顶点无法取到,故交点轨迹E的方程为![]()
![]()
(2)设![]()
![]() ,则由
,则由![]() 知,
知,![]() .
.
将![]() 代入
代入![]() 得
得![]() ,即
,即![]() ,
,
若![]() 与椭圆相切,则
与椭圆相切,则![]() ,即
,即![]() ;
;
同理若![]() 与椭圆相切,则
与椭圆相切,则![]() .
.
由![]() 与
与![]() 与轨迹E都只有一个交点包含以下四种情况:
与轨迹E都只有一个交点包含以下四种情况:
[1]直线![]() 与
与![]() 都与椭圆相切,即
都与椭圆相切,即![]() ,且
,且![]() ,消去
,消去![]() 得
得![]() ,即
,即![]() ,
,
从而![]() ,即
,即![]() ;
;
[2]直线![]() 过点
过点![]() ,而
,而![]() 与椭圆相切,此时
与椭圆相切,此时![]()
![]() ,解得
,解得![]() ;
;
[3]直线![]() 过点
过点![]() ,而
,而![]() 与椭圆相切,此时
与椭圆相切,此时![]()
![]() ,解得
,解得![]() ;
;
[4] 直线![]() 过点
过点![]() ,而直线
,而直线![]() 过点
过点![]() ,此时
,此时![]()
![]()
![]()
综上所述,h的值为![]()
(注:本题第(2)问中的“只有一个交点”不知命题的专家们指的是相交时的唯一交点还是把相切时的切点也当成是唯一的交点(严格地说,切点应该算做两个交点,只不过这两个交点重合而已),如果本题指的是严格意义上的交点,那么上述解答中只需要第四种情况,也就就是说h只能取![]() 这一个值. 如果本题将第(2)问中的“交点”改成“公共点”就不会有这种疑惑了.)
这一个值. 如果本题将第(2)问中的“交点”改成“公共点”就不会有这种疑惑了.)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 ,
, 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.  与
与 交点的轨迹E的方程
交点的轨迹E的方程 的两条直线
的两条直线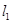 和
和 与轨迹E都只有一个交点,且
与轨迹E都只有一个交点,且 ,求
,求 的值.
的值. 分)
分) 的左、 右顶点分别为
的左、 右顶点分别为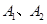 ,动直线
,动直线 与圆
与圆 相切,且与双曲线左、右两支的交点分别为
相切,且与双曲线左、右两支的交点分别为 .
.
 的取值范围,并求
的取值范围,并求 的最小值;
的最小值; 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,那么,
,那么, 是定值吗?并证明
是定值吗?并证明 的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P,
的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P, ,则
,则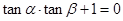 B、
B、
 D、
D、
 的左、右顶点分别为
的左、右顶点分别为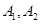 ,点
,点 ,
, 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.  与
与 交点的轨迹E的方程
交点的轨迹E的方程 和
和 与轨迹E都只有一个公共点,且
与轨迹E都只有一个公共点,且 ,求
,求 的值.
的值. 的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P,
的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P, ,则
( )
,则
( ) B.
B.
 D.
D.