题目内容
在△ABC中,内角A,B,C对边的边长分别是a,b,c.已知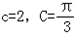 .
.
(1)若△ABC的面积等于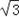 ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求△ABC的面积.
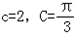 .
.(1)若△ABC的面积等于
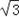 ,求a,b;
,求a,b;(2)若sinC+sin(B﹣A)=2sin2A,求△ABC的面积.
解:(1)∵c=2,C=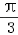 ,c2=a2+b2﹣2abcosC
,c2=a2+b2﹣2abcosC
∴a2+b2﹣ab=4,
又∵△ABC的面积等于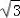 ,
,
∴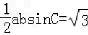 ,
,
∴ab=4
联立方程组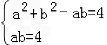 ,
,
解得a=2,b=2
(2)∵sinC+sin(B﹣A)=sin(B+A)+sin(B﹣A)=2sin2A=4sinAcosA,
∴sinBcosA=2sinAcosA
当cosA=0时,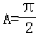 ,
,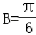 ,
,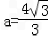 ,
,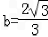 ,
,
求得此时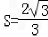
当cosA≠0时,得sinB=2sinA,
由正弦定理得b=2a,
联立方程组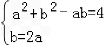
解得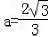 ,
,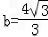 .
.
所以△ABC的面积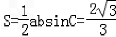
综上知△ABC的面积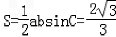
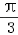 ,c2=a2+b2﹣2abcosC
,c2=a2+b2﹣2abcosC∴a2+b2﹣ab=4,
又∵△ABC的面积等于
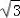 ,
,∴
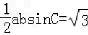 ,
,∴ab=4
联立方程组
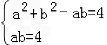 ,
,解得a=2,b=2
(2)∵sinC+sin(B﹣A)=sin(B+A)+sin(B﹣A)=2sin2A=4sinAcosA,
∴sinBcosA=2sinAcosA
当cosA=0时,
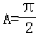 ,
,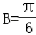 ,
,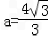 ,
,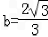 ,
,求得此时
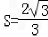
当cosA≠0时,得sinB=2sinA,
由正弦定理得b=2a,
联立方程组
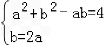
解得
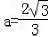 ,
,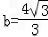 .
.所以△ABC的面积
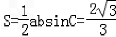
综上知△ABC的面积
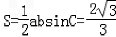

练习册系列答案
相关题目