题目内容
10.设Sn是等比数列{an}的前n项和,S3,S9,S6成等差数列.(1)设此等比数列的公比为q,求q3的值;
(2)问:数列中是否存在不同的三项am,an,ap成等差数列?若存在,求出m,n,p满足的条件;若不存在,请说明理由.
分析 (1)利用等差数列的性质、等比数列的通项公式即可得出;
(2)存在不同的三项a1,a7,a4成等差数列,例如2a7=a1+a4.
解答 解:(1)∵S3,S9,S6成等差数列,∴2S9=S3+S6,
∴(S9-S6)+(S9-S3)=0,
即(a7+a8+a9)+(a7+a8+a9)+(a4+a5+a6)=0,
∴2q3(a4+a5+a6)+(a4+a5+a6)=0,
∵${a_4}+{a_5}+{a_6}={a_4}(1+q+{q^2})≠0$,
∴${q^3}=-\frac{1}{2}$;
(2)存在不同的三项a1,a7,a4成等差数列.
∵${a_7}={a_1}{q^6}=\frac{1}{4}{a_1}$,${a_4}={a_1}{q^3}=-\frac{1}{2}{a_1}$,
∴2a7=a1+a4;
一般地,当n=m+6,且p=m+3时,有am,an,ap成等差数列.
点评 本题考查了等差数列与等比数列的通项公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.某同学用五点法画函数f(x)=Asin(ωx+ϕ),(ω>0,|ϕ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入了部分数据,如下表:
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;
(2)若函数f(x)的图象向左平移$\frac{π}{6}$个单位后对应的函数为g(x),求g(x)的图象离原点最近的对称中心.
| ωx+ϕ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | |||
| Asin(ωx+ϕ) | 0 | 5 | -5 | 0 |
(2)若函数f(x)的图象向左平移$\frac{π}{6}$个单位后对应的函数为g(x),求g(x)的图象离原点最近的对称中心.
5.已知函数f(x)=x(1+a|x|)(a∈R),设关于x的不等式f(x+a)<f(x)的解集为A,若$[{-\frac{1}{2},\frac{1}{2}}]⊆A$,则实数a的取值范围是( )
| A. | (-1,0) | B. | $({-1,\frac{{1-\sqrt{5}}}{2}})$ | C. | $({\frac{{1-\sqrt{5}}}{2},0})$ | D. | $({0,\frac{{1+\sqrt{5}}}{2}})$ |
15.设命题p:函数y=-xsinx的图象关于y轴对称,命题q:函数f(x)=x2-2x+3在区间[2,4]上的最小值是2,则下列命题中正确的是( )
| A. | p∧q | B. | ¬p∨q | C. | ¬p∧q | D. | ¬p∨¬q |
2.已知tanα,tanβ为方程x2-5x+2=0的解,则tan(α+β)的值为( )
| A. | $\frac{1}{5}$ | B. | 5 | C. | -5 | D. | -1 |

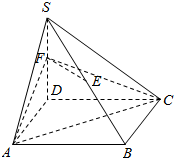 如图,四棱锥S-ABCD中,侧棱SD垂直于正方形ABCD所在的平面,E、F分别是SB、SD的中点,求证:
如图,四棱锥S-ABCD中,侧棱SD垂直于正方形ABCD所在的平面,E、F分别是SB、SD的中点,求证: