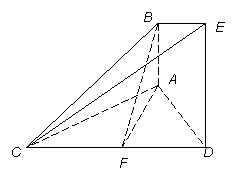
题目内容
如图,已知![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,△
,△![]() 为等边三角形,
为等边三角形,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1) 求证:![]() 平面
平面![]() ;
;
(2) 求证:平面![]() 平面
平面![]() ;
;
(3) 求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
 |
方法一:
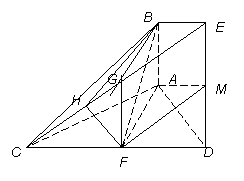
(1) 证法一:取![]() 的中点
的中点![]() ,连
,连![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 且
且![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
 |
∴![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() .
.
∴四边形![]() 为平行四边形,则
为平行四边形,则![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
证法二:取![]() 的中点
的中点![]() ,连
,连![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,
,
∴四边形![]() 为平行四边形,则
为平行四边形,则![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
又![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() . ( 5分)
. ( 5分)
(2) 证:∵![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 的中点,∴
的中点,∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,故
,故![]() 平面
平面![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() . (5分)
. (5分)
解:在平面![]() 内,过
内,过![]() 作
作![]() 于
于![]() ,连
,连![]() .
.
∵平面![]() 平面
平面![]() , ∴
, ∴![]() 平面
平面![]() .
.
∴![]() 为
为![]() 和平面
和平面![]() 所成的角.
所成的角.
设![]() ,则
,则![]() ,
,
![]() ,
,
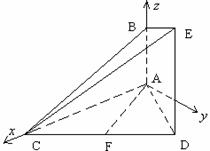
R t△![]() 中,
中,![]() .
.
∴直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() .(4分)
.(4分)
方法二:
设![]() ,建立如图所示的坐标系
,建立如图所示的坐标系![]() ,则
,则
![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴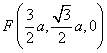 .
.
(1) 证: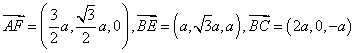 ,
,
∵![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2) 证:∵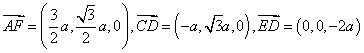 ,
,
∴![]() ,∴
,∴![]() .
.
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(3) 解:设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() 可得:
可得:
![]() ,取
,取![]() .
.
又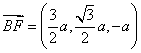 ,设
,设![]() 和平面
和平面![]() 所成的角为
所成的角为![]() ,则
,则
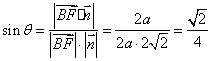 .
.
∴直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 (2013•滨州一模)如图,已知平面ABEF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=4,AB=2CD=8
(2013•滨州一模)如图,已知平面ABEF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=4,AB=2CD=8 平面
平面 ,
, 平面
平面 ,
, 为等边三角形,
为等边三角形, ,
, 为
为 中点.
中点.
 平面
平面 ;
; 平面
平面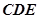 ;
; 与平面
与平面 如图,已知平面ABEF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=4,AB=2CD=8
如图,已知平面ABEF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=4,AB=2CD=8 (1)求证:
(1)求证: